高分子流体剪切带的研究进展与挑战

doi:10.7503/cjcu20250354

摘要/Abstract

摘要：

高分子流体剪切带是强剪切流场下典型的应变局域化现象, 其物理本质与调控机制是高分子流变学领域的核心科学问题. 大尺度分子动力学模拟证实, 剪切带是高分子流体在特定剪切条件下的本征行为, 常伴随稳态剪切应力平台. 最新研究揭示, 剪切带的空间位置由初始缠结网络的结构异质性决定, 平衡态下的局部缠结薄弱区(如，多重缠结稀疏区)是剪切应变集中的“种子”. 双分散体系研究进一步表明, 链长依赖性迁移与选择性富集形成的“快带软化-慢带硬化”动态耦合机制是剪切带稳定的关键. 本文综合评述了高分子流体剪切带的研究进展, 重点讨论其本征性、形成机理、动态演化及稳定性; 总结了关于剪切带研究的主要争议与挑战；展望了未来研究方向, 强调通过发展高时空分辨原位表征技术、深化多尺度模拟与理论, 实现剪切带的有效预测与调控, 将为指导高分子材料的精密成型(如，注塑、挤出过程中的流变均匀性控制以及超薄膜、超细纤维等先进制品的可控制备)提供关键理论支撑, 从而显著提升加工效率与产品性能.

关键词: 剪切带, 非线性流变学, 缠结, 应变局域化, 分子动力学

Abstract:

Shear banding in polymer fluids represents a paradigmatic example of strain localization under strong nonlinear shear flow， with its physical origin and regulatory mechanisms standing as central scientific questions in polymer rheology. Large-scale molecular dynamics simulations have firmly established shear banding as an intrinsic bulk phenomenon under specific shear conditions， often accompanied by a stress plateau in the steady-state shear stress-shear rate curve. Emerging studies reveal that the spatial localization of shear bands is determined by the initial structural heterogeneity of the entanglement network， where pre-existing "weak spots" in the equilibrium state， such as regions with sparse multiple entanglements， act as nucleation sites for shear stain concentration. Investigations on bidisperse systems further demonstrate that chain-length-dependent migration and selective enrichment drive a "fast-band softening-slow-band hardening" coupling mechanism， which is critical for the long-term stability of shear bands. This review synthesizes recent advances in understanding shear banding， focusing on its intrinsic nature， formation mechanisms， dynamic evolution， and stability， and summarizes the key controversies， challenges， and future research directions in shear band studies. It emphasizes that achieving effective prediction and regulation of shear bands， through the development of high spatiotemporal resolution in-situ characterization techniques and the advancement of multi-scale simulations and theories， will provide critical theoretical support for guiding the precision forming of polymeric materials. This includes controlling rheological uniformity in processes such as injection molding and extrusion， as well as enabling the controlled fabrication of advanced products like ultra-thin films and ultra-fine fibers， thereby significantly enhancing processing efficiency and product performance.

Key words: Shear banding, Nonlinear rheology, Entanglement, Strain localization, Molecular dynamics

中图分类号:

O631

TrendMD:

卢宇源, 安立佳. 高分子流体剪切带的研究进展与挑战. 高等学校化学学报, 2026, 47(1): 20250354.

LU Yuyuan, AN Lijia. Progress and Challenges in Shear Banding of Polymer Fluids. Chem. J. Chinese Universities, 2026, 47(1): 20250354.

图/表 9

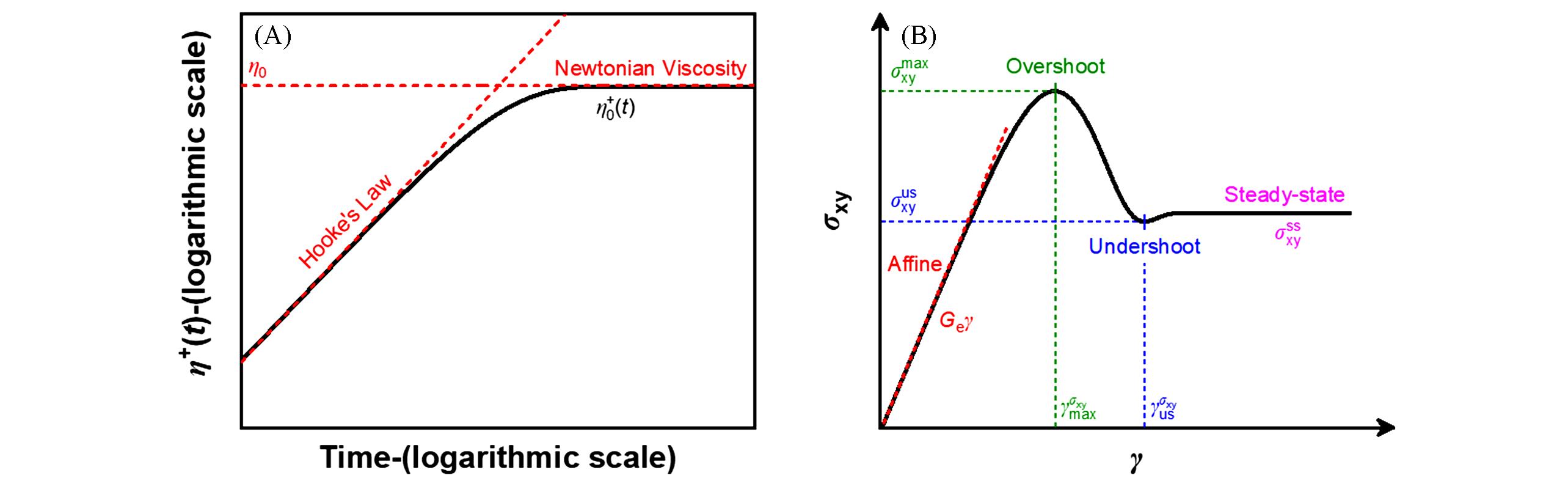
Fig.1 Comparison of the instantaneous shear viscosity of entangled polymeric fluids at low shear rates with those of ideal elastic solids and ideal viscous liquids(A), and the shear stress(σxy ) of the polymeric fluid as a function of the strain(γ)(B)[11]（B） When the shear rate exceeds 1/τR（τR is the Rouse relaxation time）， the σxy of the polymeric fluid exhibits complex viscoelastic characteristics with increasing strain γ.

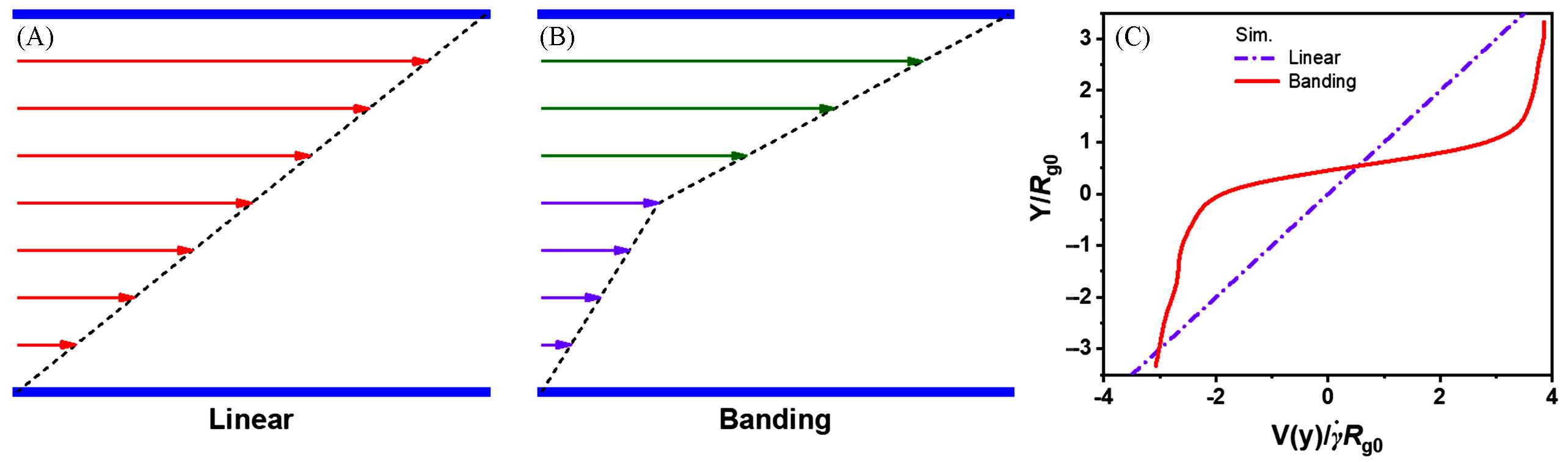
Fig.2 Schematic illustration of a linear flow field(A), schematic of shear banding(B) and flow field distribution from molecular dynamics simulations under shear(C)[11]（A） Where the shear rate is uniform along the gradient direction；（B） the flow field is divided into a fast（green） streamlines and a slow（purple） streamlines layer. Rg0： radius of gyration.

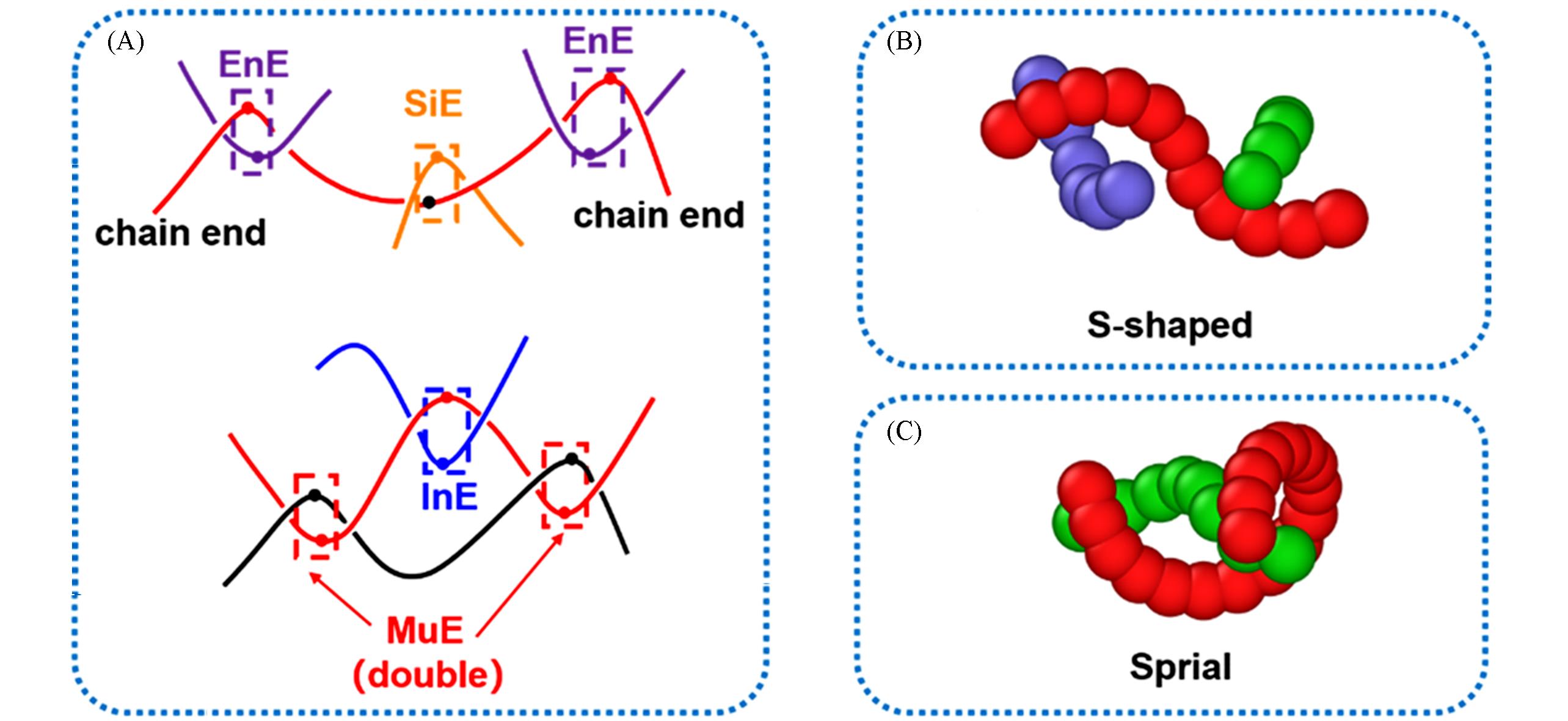
Fig.3 Schematic representation of distinct entanglement types identified via the FT⁃PPA method: End entanglements(EnE, purple), simple entanglements(SiE, yellow), intervening entanglements(InE, blue), and multiple(double) entanglements(MuE, red)(A), typical chain conformations illustrating "S⁃shaped kinks"(B) and "sprial kinks" observed in the simulations(C)[70]（A） The red line denotes the primitive path（PP） of the target chain， with other colored lines representing PPs of surrounding chains that entangle with it.（B） S-shaped kinks arise when a target chain forms entanglements with two opposing chains， leading to a local reversal in PP curvature， resulting in a near-zero average curvature over that segment. Sprial kinks occur when two PPs intertwine through more than one complete revolution， adopting an approximately spiral configuration along their lengths.Copyright 2024， American Chemical Society.

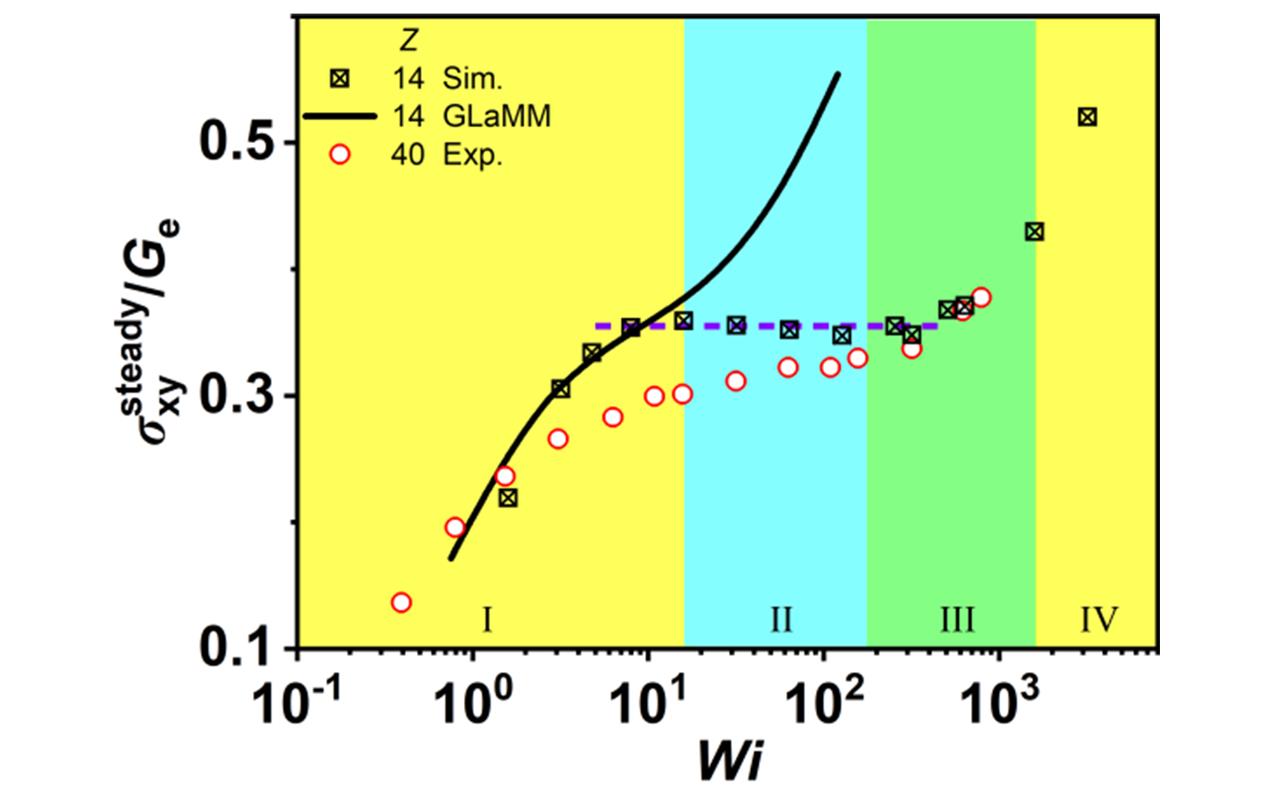
Fig.4 Normalized steady⁃state shear stress σxysteady/Ge(the plateau modulus) as a function of the Weissenberg number(Wi)[30]The black line and red points correspond to the GLaMM theory［44］ and experimental results［17］， respectively. Based on the measurements， the shear rate can be divided into four regimes： regime I（yellow） without shear banding（velocity field remains linear）； regime II（cyan） with steady shear banding； regime III（green） with transient shear banding； regime IV（yellow） without shear banding. Extremely weak shear bands exist at the shear rates Wi=16.0 and Wi=1595 corresponding to the boundaries of regimes I/II and III/IV.Copyright 2021， American Chemical Society.

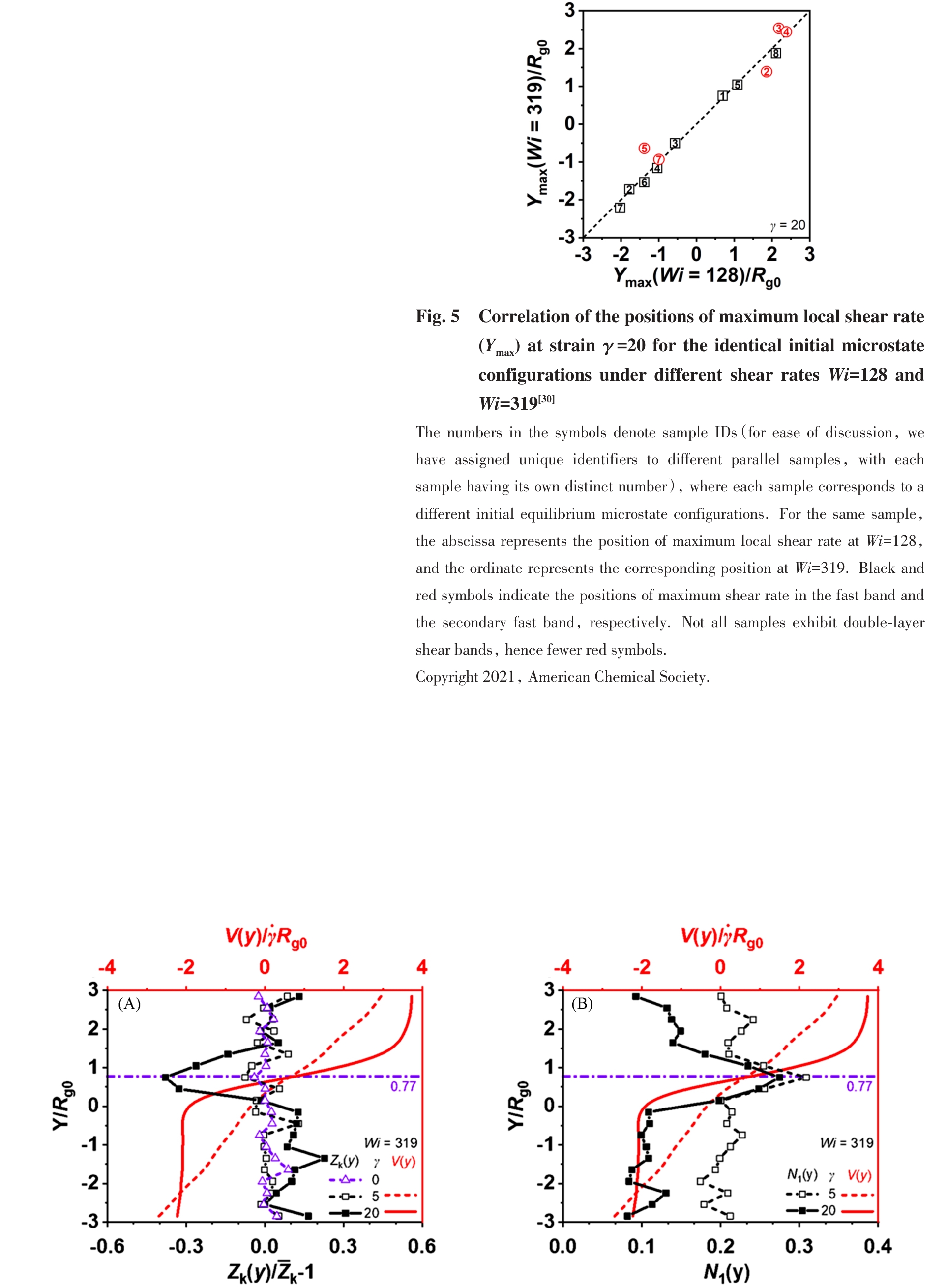
Fig.6 Comparison of the average number of entanglements per chain Zk(y) distribution(A) and the first normal stress N1(y) distribution with the velocity V(y) distribution at Wi=319(B)[30]The purple line indicates the position of the minimum Zk or maximum N1.Copyright 2021， American Chemical Society.

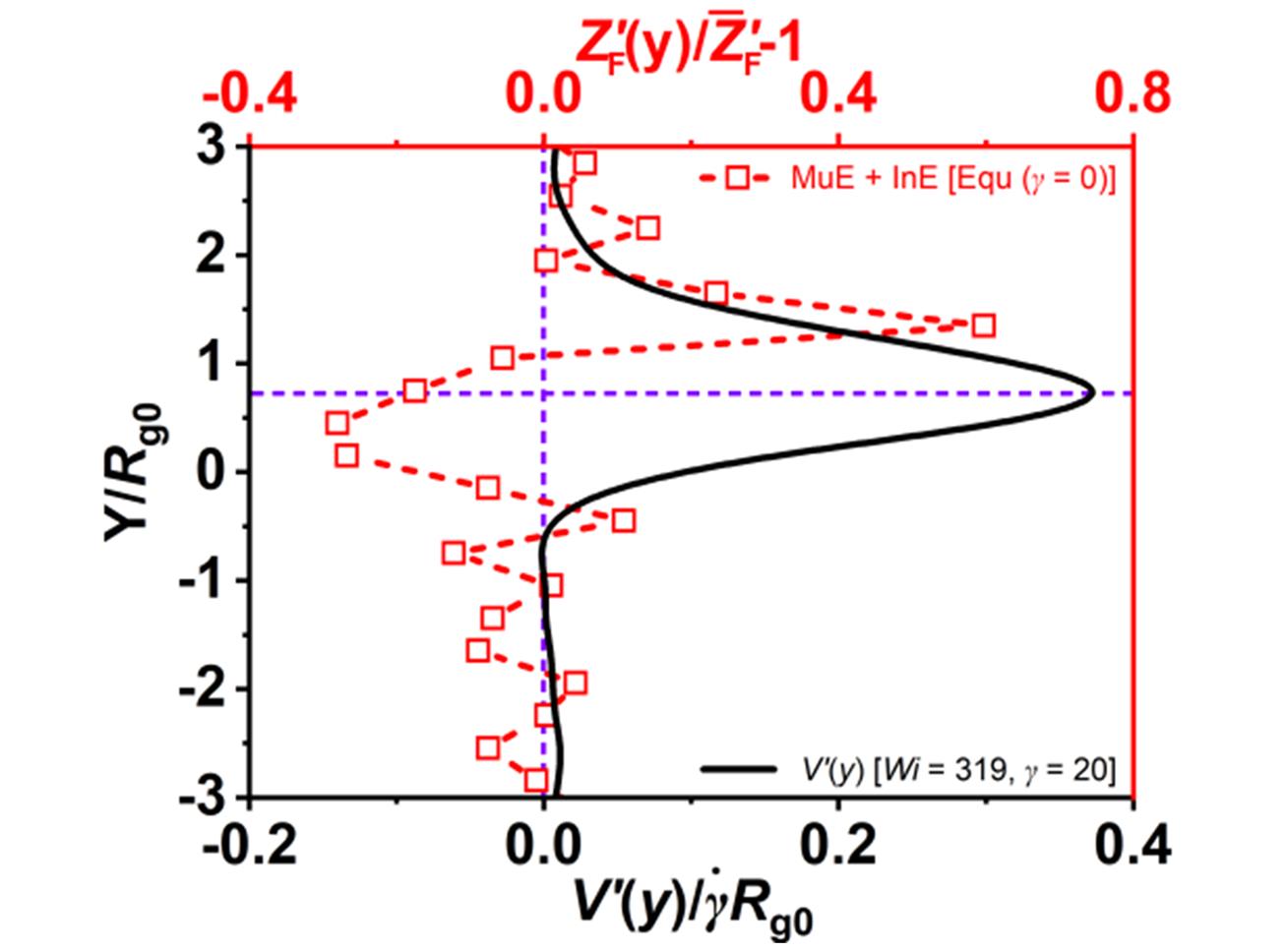
Fig.7 Shear rate V′(y) distribution along the gradient direction(left panel, black line) under the conditions of Wi=319 and strain γ=20 and the distribution of MuEs and InEs[Z′F(y)] for the same sample at equilibrium(γ=0, right panel, red line)[70]Copyright 2024， American Chemical Society.

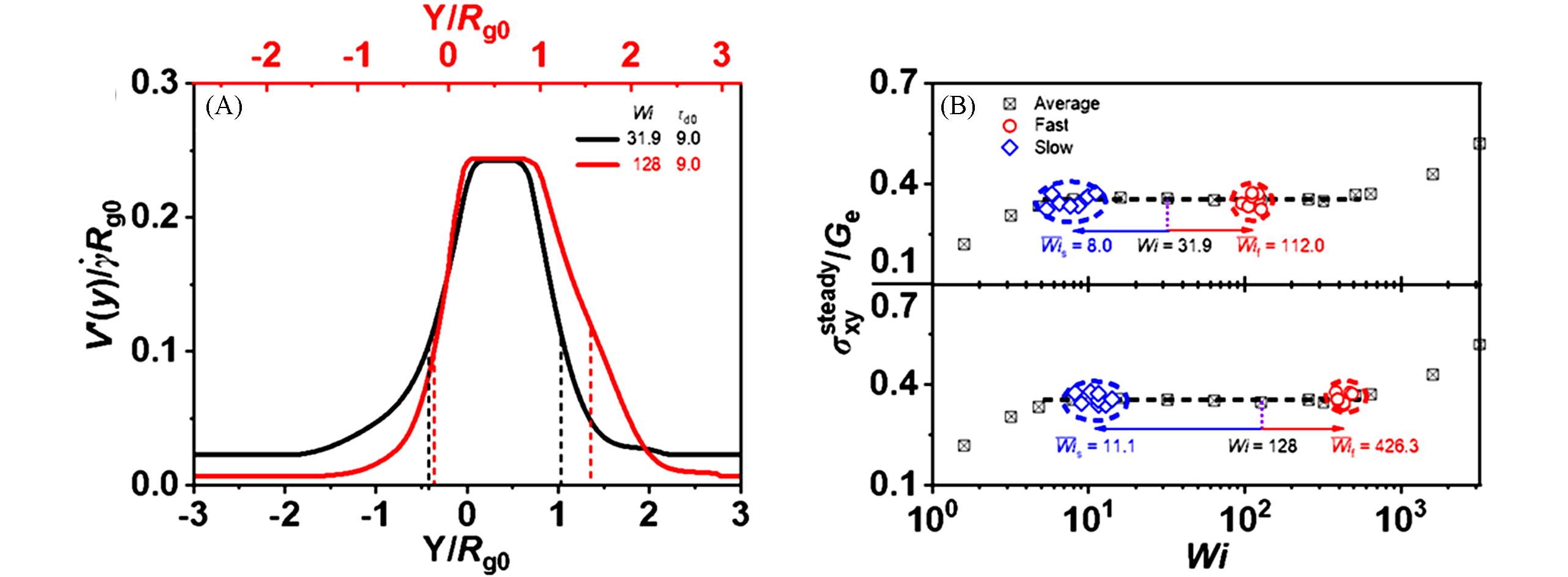
Fig.8 Normalized local shear rate for a sample at Wi=31.9 and Wi=128(A), local shear rates Wif/s in the fast/slow shear bands for different samples at Wi=31.9 and Wi=128(Wif/s ≡ τdγ˙f/s)(B)[30]（A） The corresponding dashed line represents the interface between the fast and slow shear bands. The nearly identical curve heights under different shear rates indicate that the local shear rate in the fast band is proportional to the applied shear rate. （B） Due to sample-to-sample variations， data points from different samples do not perfectly overlap. Copyright 2021， American Chemical Society.

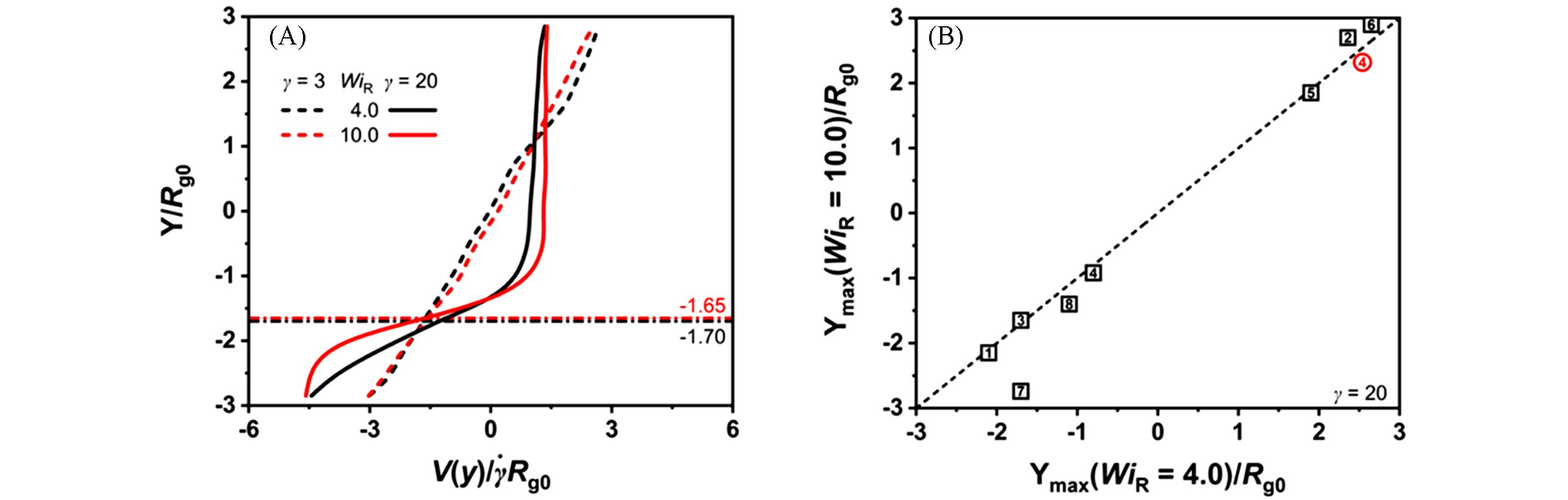
Fig.9 Velocity distribution curves of a bidisperse mixture(N200/N400) at shear rates WiR=4.0(black) and WiR=10.0(red) for strains γ=3(dashed lines) and γ=20(solid lines)(A), sample⁃to⁃sample correlation function of Ymax between WiR=4.0 and WiR=10.0 at strain γ=20 for 8 independent samples(B)[41]（A） The dash-dotted line indicates the position of the center of the fast shear band. The velocity profile remains approximately linear before the stress overshoot（dashed lines）， indicating uniform flow. After the stress overshoot， distinct shear bands form（solid lines）.（B）The numbers in the symbols denote sample IDs（for ease of discussion， we have assigned unique identifiers to different parallel samples， with each sample having its own distinct number）. For the same sample， the abscissa is Ymax at WiR=4.0， and the ordinate is the corresponding position at WiR=10.0. Black and red symbols represent the positions of maximum shear rate in the fastest and secondary fast bands， respectively. Only one sample exhibits double-layer shear bands， hence only one red symbol.Copyright 2025， Springer Nature.

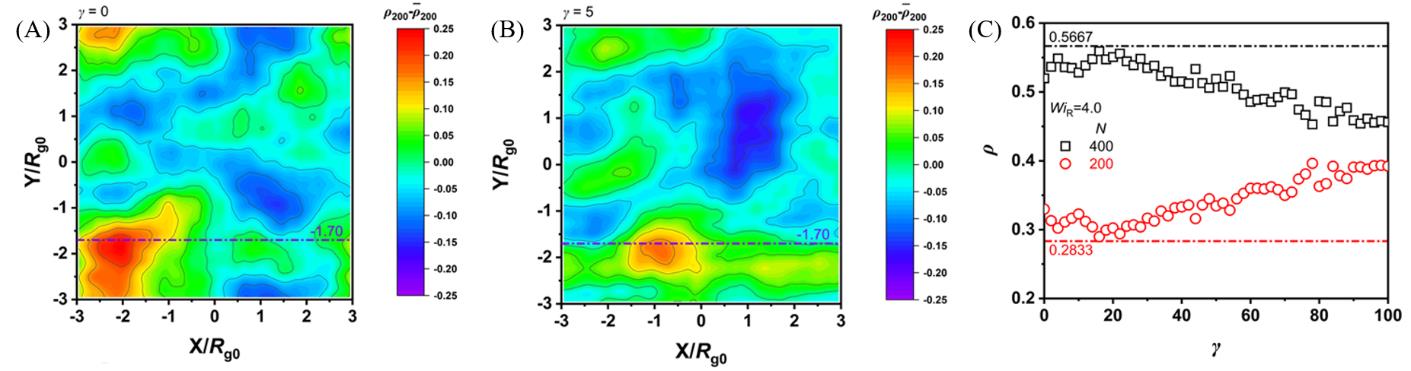
Fig.10 Two⁃dimensional distribution of the number density of short⁃chain monomers in the vorticity plane at strains γ=0(A) and γ=5(B), with a slice thickness equal to the root⁃mean⁃square radius of gyration (Rg0), variation of monomer number density ρ of short chains N=200 and long chains N=400 at the center of the fast shear band with strain γ under WiR=4.0(C)[41]（C） The dash-dotted lines represent the average monomer number densities of short chains N=200（circles）， and long chains N=400（squares） in the sample N200/N400. Note that since the number of short and long chains is equal， the average monomer number density of long chains is twice that of short chains.Copyright 2025， Springer Nature.

参考文献 102

[1]	Rubinstein M.， Colby R. H.， Polymer Physics， Oxford University Press， New York， 2003
[2]	Dealy J. M.， Larson R. G.， Structure and Rheology of Molten Polymers： from Structure to flow Behavior and Back Again， Hanser Publishers， Munich， 2006
[3]	Wang S. Q.， Nonlinear Polymer Rheology： Macroscopic Phenomenology and Molecular Foundation， John Wiley & Sons， Hoboken， 2018
[4]	Malkin A. Y.， Rheology Fundamental， ChemTec Publishing， Toronto， 1994
[5]	Macosko C. W.， Rheology： Principles， Measurements and Applications， Wiley⁃VCH， New York， 1994
[6]	Morrison F. A.， Understanding Rheology， Oxford University Press， New York， 2001
[7]	Doi M.， Edwards S. F.， The Theory of Polymer Dynamics， Oxford University Press， New York， 1986
[8]	Lu Y.， An L.， Wang J.， Acta Polym. Sin.， 2016， 47， 688—697
[9]	Ruan Y.， Wang Z.， Lu Y.， An L.， Acta Polym. Sin.， 2017， 5， 727—743
[10]	Ruan Y.， Lu Y.， An L.， Acta Polym. Sin.， 2018， 12， 1493—1506
[11]	Ma L. C.， Mechanistic Investigation of Nonlinear Rheological Behavior in Entangled Polymer Fluids During Start⁃up Shear via Molecular Dynamics Simulation， University of Science and Technology of China， Hefei， 2025
	马立成. 启动剪切下缠结高分子流体非线性流变行为的分子动力学模拟与分子机理研究，合肥：中国科学技术大学， 2025
[12]	Tapadia P.， Wang S. Q.， Phys. Rev. Lett.， 2006， 96， 016001
[13]	Wang S. Q.， Ravindranath S.， Boukany P.， Olechnowicz M.， Quirk R. P.， Halasa A.， Mays J.， Phys. Rev. Lett.， 2006， 97， 187801
[14]	de Gennes P. G.， European Phys. J. E， 2007， 23， 3
[15]	Hatzikiriakos S. G.， Prog. Polym. Sci.， 2012， 37， 624—643
[16]	Olmsted P. D.， Rheologica Acta， 2008， 47， 283—300
[17]	Wang S. Q.， Ravindranath S.， Boukany P. E.， Macromolecules， 2011， 44， 183—190
[18]	Ravindranath S.， Wang S. Q.， J. Rheology， 2008， 52， 957—980
[19]	Divoux T.， Fardin M. A.， Manneville S.， Lerouge S.， Shear Banding of Complex Fluids， in Annual Review of Fluid Mechanics， Davis S. H.， Moin P.， Eds.， Annual Reviews， Palo Alto， 2016， 48， 81—103
[20]	Fielding S. M.， Soft Matter， 2007， 3， 1262—1279
[21]	Wang S. Q.， Macromol. Chem. Phys.， 2019， 220， 1800327
[22]	Doi M.， Edwards S. F.， J. Chem. Soc.， Faraday Transactions 2： Mole. Chem. Phys.， 1978， 74， 1789—1801
[23]	Doi M.， Edwards S. F.， J. Chem. Soc.， Faraday Transactions 2： Mole. Chem. Phys.， 1978， 74， 1802—1817
[24]	Doi M.， Edwards S. F.， J. Chem. Soc.， Faraday Transactions 2： Mole. Chem. Phys.， 1978， 74， 1818—1832
[25]	Doi M.， Edwards S. F.， J. Chem. Soc.， Faraday Transactions 2： Mole. Chem. Phys.， 1979， 75， 38—54
[26]	Wang S. Q.， Macromol. Mater. Eng.， 2007， 292， 15—22
[27]	Burroughs M. C.， Zhang Y.， Shetty A. M.， Bates C. M.， Leal L. G.， Helgeson M. E.， Phys. Rev. Lett.， 2021， 126， 207801
[28]	Wang Z.， Lam C. N.， Chen W. R.， Wang W.， Liu J.， Liu Y.， Porcar L.， Stanley C. B.， Zhao Z.， Hong K.， Wang Y.， Phys. Rev. X， 2017， 7， 031003
[29]	Cao J.， Likhtman A. E.， Phys. Rev. Lett.， 2012， 108， 028302
[30]	Ruan Y.， Lu Y.， An L.， Wang Z. G.， ACS Macro Lett.， 2021， 10， 1517—1523
[31]	Fielding S. M.， Olmsted P. D.， Phys. Rev. E， 2003， 68， 036313
[32]	Fielding S. M.， Phys. Rev. Lett.， 2005， 95， 134501
[33]	Adams J. M.， Olmsted P. D.， Phys. Rev. Lett.， 2009， 102， 067801
[34]	Adams J. M.， Fielding S. M.， Olmsted P. D.， J. Rheol.， 2011， 55， 1007—1032
[35]	Cromer M.， Villet M. C.， Fredrickson G. H.， Leal L. G.， Phys. Fluids， 2013， 25， 051703
[36]	Cromer M.， Fredrickson G. H.， Leal L. G.， Phys. Fluids， 2014， 26， 063101
[37]	Peterson J. D.， Cromer M.， Fredrickson G. H.， Leal L. G.， J. Rheol.， 2016， 60， 927—951
[38]	Li Y.， Hu M.， McKenna G. B.， Dimitriou C. J.， McKinley G. H.， Mick R. M.， Venerus D. C.， Archer L. A.， J. Rheol.， 2013， 57， 1411—1428
[39]	Li Y.， Hu M.， McKenna G. B.， Dimitriou C. J.， McKinley G. H.， Mick R. M.， Venerus D. C.， Archer L. A.， J. Rheol.， 2014， 58， 1071—1082
[40]	Ma L. C.， Ruan Y. J.， Wang Z. H.， Lu Y. Y.， An L. J.， Chinese J. Polym. Sci.， 2024， 42， 1811—1823
[41]	Ma L. C.， Ruan Y. J.， Lu Y. Y.， An L. J.， Chinese J. Polym. Sci.， 2025， 43， 2150—2159
[42]	Marrucci G.， Grizzuti N.， J. Rheol.， 1983， 27， 433—450
[43]	Mead D. W.， Larson R. G.， Doi M.， Macromolecules， 1998， 31， 7895—7914
[44]	Likhtman A. E.， McLeish T. C. B.， Macromolecules， 2002， 35， 6332—6343
[45]	Graham R. S.， Likhtman A. E.， McLeish T. C. B.， Milner S. T.， J. Rheol.， 2003， 47， 1171—1200
[46]	Likhtman A. E.， Graham R. S.， J. Non⁃Newton. Fluid Mech.， 2003， 114， 1—12
[47]	Xie S. J.， Schweizer K. S.， Macromolecules， 2018， 51， 4185—4200
[48]	Schweizer K. S.， Xie S. J.， ACS Macro Lett.， 2018， 7， 218—222
[49]	de Gennes P. G.， J. Chem. Phys.， 1971， 55， 572—579
[50]	Osaki K.， Inoue T.， Isomura T.， J. Polym. Sci. Part B： Polym. Phys.， 2000， 38， 1917—1925
[51]	Osaki K.， Inoue T.， Uematsu T.， J. Polym. Sci. Part B： Polym. Phys.， 2000， 38， 3271—3276
[52]	Pearson D. S.， Kiss A. D.， Fetters L. J.， Doi M.， J. Rheol.， 1989， 33， 517—535
[53]	McLeish T. C. B.， Ball R. C.， J. Polym. Sci. Part B： Polym. Phys.， 1986， 24， 1735—1745
[54]	McLeish T. C. B.， J. Polym. Sci. Part B： Polym. Phys.， 1987， 25， 2253—2264
[55]	Ianniruberto G.， Marrucci G.， Masubuchi Y.， Macromolecules， 2020， 53， 5023—5033
[56]	Doi M.， J. Polym. Sci.： Polym. Phys. Ed.， 1983， 21， 667—684
[57]	Viovy J. L.， Rubinstein M.， Colby R. H.， Macromolecules， 1991， 24， 3587—3596
[58]	Marrucci G.， J. Non⁃Newton. Fluid Mech.， 1996， 62， 279—289
[59]	Spenley N. A.， Cates M. E.， McLeish T. C. B.， Phys. Rev. Lett.， 1993， 71， 939—942
[60]	Britton M. M.， Callaghan P. T.， Phys. Rev. Lett.， 1997， 78， 4930—4933
[61]	Callaghan P. T.， Gil A. M.， Macromolecules， 2000， 33， 4116—4124
[62]	Boukany P. E.， Wang S. Q.， Soft Matter， 2009， 5， 780—789
[63]	Wang S. Q.， Ravindranath S.， Wang Y.， Boukany P.， J. Chem. Phys.， 2007， 127， 064903
[64]	Hemingway E. J.， Fielding S. M.， Phys. Rev. Lett.， 2018， 120， 138002
[65]	Hu Y. T.， Wilen L.， Philips A.， Lips A.， J. Rheol.， 2007， 51， 275—295
[66]	Hu Y. T.， J. Rheol.， 2010， 54， 1307—1323
[67]	Hayes K. A.， Buckley M. R.， Cohen I.， Archer L. A.， Phys. Rev. Lett.， 2008， 101， 218301
[68]	Wang S. Q.， Wang Y.， Cheng S.， Li X.， Zhu X.， Sun H.， Macromolecules， 2013， 46， 3147—3159
[69]	Fielding S. M.， J. Rheol.， 2016， 60， 821—834
[70]	Ruan Y.， Lu Y.， An L.， Wang Z. G.， Macromolecules， 2024， 57， 2792—2800
[71]	Schieber J. D.， Neergaard J.， Gupta S.， J. Rheol.， 2003， 47， 213—233
[72]	Schieber J. D.， J. Chem. Phys.， 2003， 118， 5162—5166
[73]	Schieber J. D.， Andreev M.， Annu. Rev. Chem. Biomol. Engineer.， 2014， 5， 367—381
[74]	Steenbakkers R. J. A.， Tzoumanekas C.， Li Y.， Liu W. K.， Kröger M.， Schieber J. D.， New J. Phys.， 2014， 16， 015027
[75]	Likhtman A. E.， Macromolecules， 2005， 38， 6128—6139
[76]	Masubuchi Y.， Takimoto J. I.， Koyama K.， Ianniruberto G.， Marrucci G.， Greco F.， J. Chem. Phys.， 2001， 115， 4387—4394
[77]	Chappa V. C.， Morse D. C.， Zippelius A.， Müller M.， Phys. Rev. Lett.， 2012， 109， 148302
[78]	Uneyama T.， Masubuchi Y.， J. Chem. Phys.， 2012， 137， 154902
[79]	Kremer K.， Grest G. S.， J. Chem. Phys.， 1990， 92， 5057—5086
[80]	Lee W. B.， Kremer K.， Macromolecules， 2009， 42， 6270—6276
[81]	Ramírez J.， Sukumaran S. K.， Vorselaars B.， Likhtman A. E.， J. Chem. Phys.， 2010， 133， 154103
[82]	Kröger M.， Hess S.， Phys. Rev. Lett.， 2000， 85， 1128—1131
[83]	Xu X.， Chen J.， An L.， J. Chem. Phys.， 2014， 140， 174902
[84]	Cao J.， Likhtman A. E.， ACS Macro Lett.， 2015， 4， 1376—1381
[85]	Everaers R.， Sukumaran S. K.， Grest G. S.， Svaneborg C.， Sivasubramanian A.， Kremer K.， Science， 2004， 303， 823—826
[86]	Sukumaran S. K.， Grest G. S.， Kremer K.， Everaers R.， J. Polymer Science Part B： Polym. Phys.， 2005， 43， 917—933
[87]	Hsu H. P.， Kremer K.， ACS Macro Lett.， 2018， 7， 107—111
[88]	Hsu H. P.， Kremer K.， Macromolecules， 2019， 52， 6756—6772
[89]	Kröger M.， Comput. Phys. Commun.， 2005， 168， 209—232
[90]	Shanbhag S.， Kröger M.， Macromolecules， 2007， 40， 2897—2903
[91]	Kröger M.， Dietz J. D.， Hoy R. S.， Luap C.， Comput. Phys. Commun.， 2023， 283， 108567
[92]	Tzoumanekas C.， Theodorou D. N.， Macromolecules， 2006， 39， 4592—4604
[93]	Anogiannakis S. D.， Tzoumanekas C.， Theodorou D. N.， Macromolecules， 2012， 45， 9475—9492
[94]	Sliozberg Y. R.， Yeh I. C.， Kröger M.， Masser K. A.， Lenhart J. L.， Andzelm J. W.， Macromolecules， 2018， 51， 9635—9648
[95]	Ben⁃Naim E.， Grest G. S.， Witten T. A.， Baljon A. R. C.， Phys. Rev. E， 1996， 53， 1816—1822
[96]	Likhtman A. E.， Ponmurugan M.， Macromolecules， 2014， 47， 1470—1481
[97]	Cao J.， Qin J.， Milner S. T.， Macromolecules， 2015， 48， 99—110
[98]	Baig C.， Mavrantzas V. G.， Kröger M.， Macromolecules， 2010， 43， 6886—6902
[99]	Hass J.， Heil C.， Weir M.， Thomas’ Calculus， 14th Ed.， Pearson， Boston， 2017
[100]	Shin S.， Kou Y.， Dorfman K. D.， Cheng X.， Macromolecules， 2021， 54， 4186—4197
[101]	Olmsted P. D.， Radulescu O.， Lu C. Y. D.， J. Rheol.， 2000， 44， 257—275
[102]	Foteinopoulou K.， Karayiannis N. C.， Mavrantzas V. G.， Kröger M.， Macromolecules， 2006， 39， 4207—4216