黄铜矿型铜基硫属半导体材料的电子结构和光学性质

doi:10.7503/cjcu20180550

摘要/Abstract

摘要：

采用基于赝势平面波基组的密度泛函理论方法, 对具有黄铜矿结构的6种CuXY₂(X=Ga, In; Y=S, Se, Te)晶体的构型、电子结构、线性及二阶非线性光学性质进行了研究. 结果表明, 6种CuXY₂均为直接带隙半导体, 具有相似的能带结构. 当X原子相同时, 随着Y原子按S→Se→Te依次改变时, 体系的静态介电常数、静态折射率和静态倍频系数(d₃₆)依次递增. 在占据带中, 位于价带顶附近的能带对体系倍频效应影响最为显著, 该系列化合物的能带主要成分为Cu的3d轨道和Y原子价层p轨道; 对于空能带, 对倍频系数影响较大的是以X原子价层p轨道为主要成分的能带. 6种晶体中, CuInSe₂晶体具有较高的光电导率并对太阳光具有较好的吸收性能. 综合考虑体系的双折射率和倍频效应等因素, CuGaS₂和CuGaSe₂ 2种晶体在二阶非线性光学领域具有潜在的应用价值.

关键词: 密度泛函理论, 电子结构, 光学性质, 倍频系数, 黄铜矿

Abstract:

The density functional theory(DFT) based on the pseudo-potential plane wave basis was employed to investigate the geometries, electronic structures, linear and second-order nonlinear optical properties of the CuXY₂(X=Ga, In; Y=S, Se, Te) crystals with chalcopyrite structure. The results indicate that these compounds are semiconductors with a direct gap and have similar band structures. The static dielectric constants, the refractive indices and the second harmonic generation(SHG) coefficients(d₃₆) of these compounds increase in the sequence of S→Se→Te for the same X atom. Among the occupied bands, those states near the top of the valence band contribute mostly to the SHG effect, which are dominated by the components of C $u 3 d$ orbitals and the valence p orbitals of Y atom. While for the unoccupied bands, the bands mainly derived from valence p orbitals of X atoms have obvious influences on the SHG coefficient. Among these six crystals, CuInSe₂ has high photoconductivity and better absorption of sunlight. In addition, CuGaS₂ and CuGaSe₂ crystal have potential applications in the second-order nonlinear optical fields based on their birefringences and SHG strengths.

Key words: Density functional theory(DFT), Electronic structure, Optical property, Second harmonic generation, Chalcopyrite

中图分类号:

O641

周和根, 金华, 郭辉瑞, 林晶, 章永凡. 黄铜矿型铜基硫属半导体材料的电子结构和光学性质[J]. 高等学校化学学报, 2019, 40(3): 518-527.

ZHOU Hegen,JIN Hua,GUO Huirui,LIN Jing,ZHANG Yongfan. Electronic Structures and Optical Properties of Cu-based Semiconductors with Chalcopyrite-type Structure^†[J]. Chemical Journal of Chinese Universities, 2019, 40(3): 518-527.

图/表 15

Fig.1 Unit cell of CuXY2 crystal with chalcopyrite structure

Table 1 Experimental and theoretical results of cell parameters and band gaps of CuXY2 crystals

Crystal	a/nm		c/nm		Volume/nm³		E_g/eV		Ref.	Scissor/eV
Crystal	Exp.	Cal.	Exp.	Cal.	Exp.	Cal.	Exp.	Cal.	Ref.	Scissor/eV
CuGaS₂	0.5360	0.5368	1.0491	1.0561	0.2995	0.3069	2.43	0.669	[14]	1.761
CuGaSe₂	0.5614	0.5667	1.1022	1.1258	0.3474	0.3615	1.68	0.053	[31]	1.627
CuGaTe₂	0.6024	0.6083	1.1940	1.2156	0.4332	0.4498	1.24	0.225	[32]	1.015
CuInS₂	0.5523	0.5592	1.1122	1.1243	0.3392	0.3516	1.53	0.022	[33]	1.508
CuInSe₂	0.5782	0.5874	1.1617	1.1786	0.3884	0.4067	1.04	0.015	[34]	1.025
CuInTe₂	0.6194	0.6283	1.2416	1.2621	0.4764	0.4982	1.06	0.001	[35]	1.059

Fig.2 Band structures of CuGaTe2(A) and CuInTe2(B) crystals The Fermi level(EF) is set to the top of valence bands.

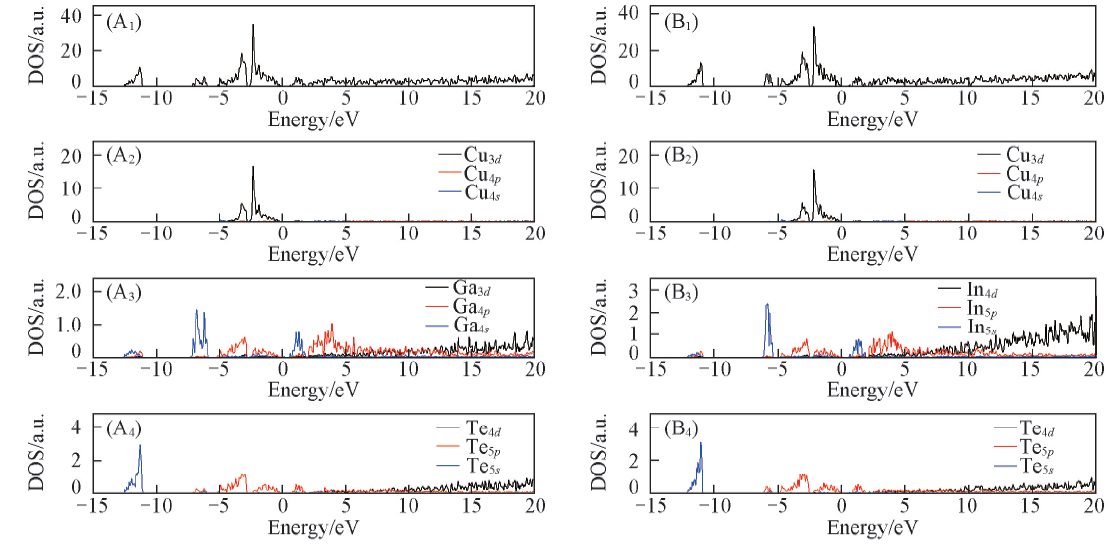
Fig.3 Total and partial density of states(DOSs) of CuGaTe2(A1—A4) and CuInTe2(B1—B4) crystals (A1, B1) Total; (A2, B2) Cu; (A3) Ga; (B3) In; (A4, B4) Te. The zero energy is set to Fermi level(EF).

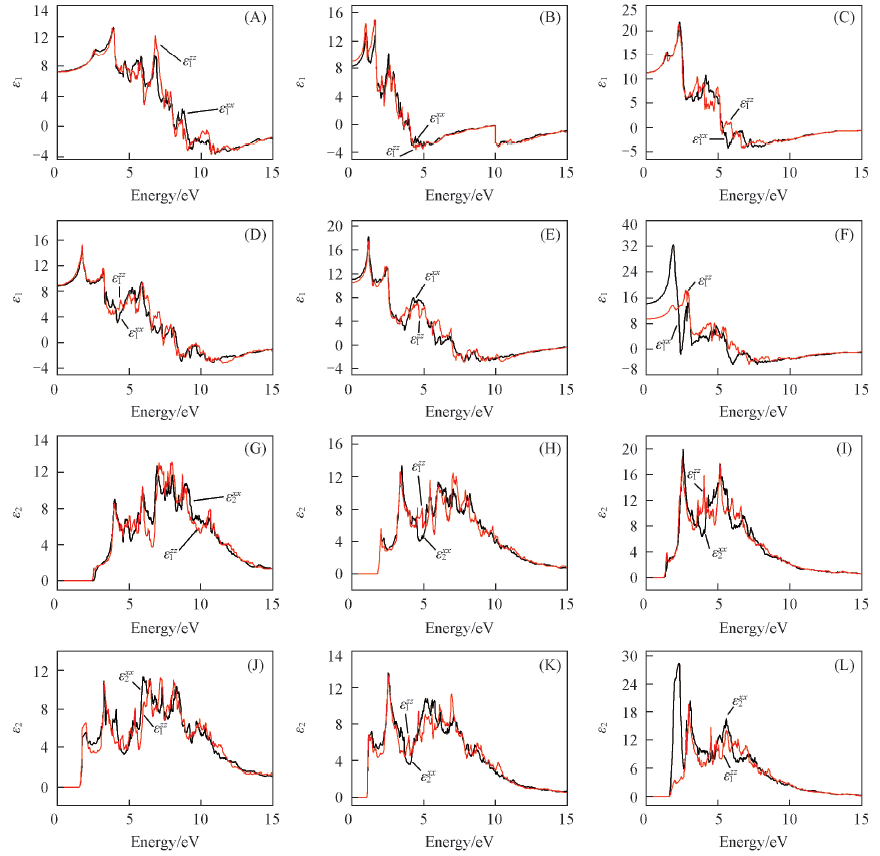
Fig.4 Variations of the real part(A)—(F) and imaginary part(G)—(L) of dielectric function of CuXY2 crystals(A, G) CuGaS2; (B, H) CuGaSe2; (C, I) CuGaTe2; (D, J) CuInS2; (E, K) CuInSe2; (F, L) CuInTe2.

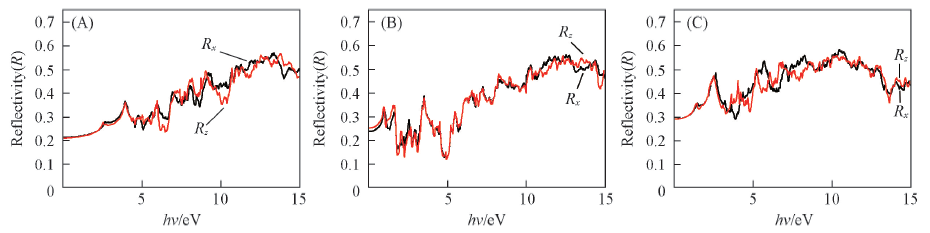
Fig.5 Variations of the refractive index and birefringence of CuGaS2(A),CuGaSe2(B) and CuGaTe2(C) crystals

Fig.6 Variations of reflectivity of CuGaS2(A), CuGaSe2(B) and CuGaTe2(C) crystals Rx and Rz are the reflectivity along x and z directions, respectively.

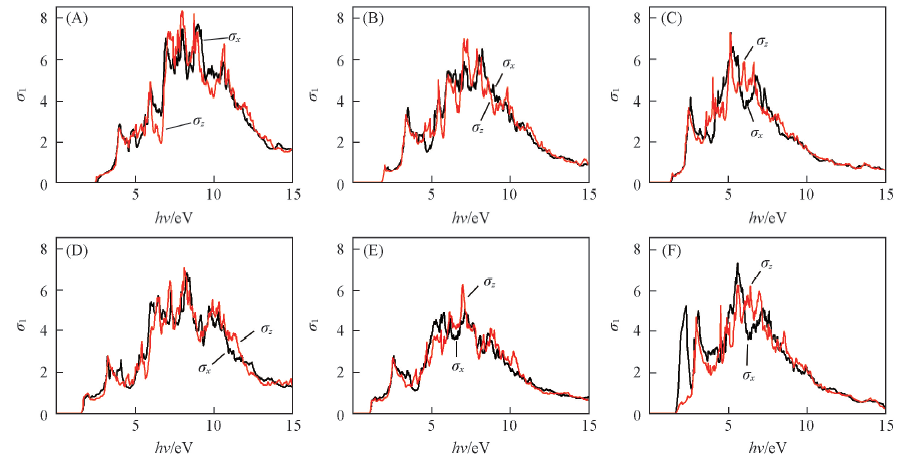
Fig.7 Variations of real part of photoconductivity of CuGaS2(A), CuGaSe2(B), CuGaTe2(C), CuInS2(D), CuInSe2(E) and CuInTe2(F) crystalsσx and σz are the photoconductivity along x and z directions, respectively.

Table 2 Experimental and theoretical values of refractive index and d36 of CuXY2 crystals

Crystal	Refractive index at zero frequency			d₃₆/(pm·V^-1) at wavelength of 10.6 μm
Crystal	This work	Other works	Exp.	This work	Other works	Exp.
CuGaS₂	2.70	2.77^[16]	2.5—3.05^[38]	13.06	11.35^[15]	14.5±15%^[40]
		2.62^[36]	2.2—2.9^[39]
CuGaSe₂	2.93	3.69^[16]	2.34—3.38^[38]	28.74	27.75^[15]	30.0±10%^[40]
		2.82^[36]
CuGaTe₂	3.35	4.99^[16]		114.87	70.00^[15]
CuInS₂	2.98	3.22^[16]	2.38—2.82^[38]	17.87	15.85^[15]	10.6±15%^[40]
		2.76^[36]	1.6—3^[39]
CuInSe₂	3.32	3.54^[16]	2.04—3.12^[38]	60.16	36.25^[15]
		3.10^[36]
CuInTe₂	3.76	4.98^[16]		82.02	63.00^[15]
		3.05^[37]

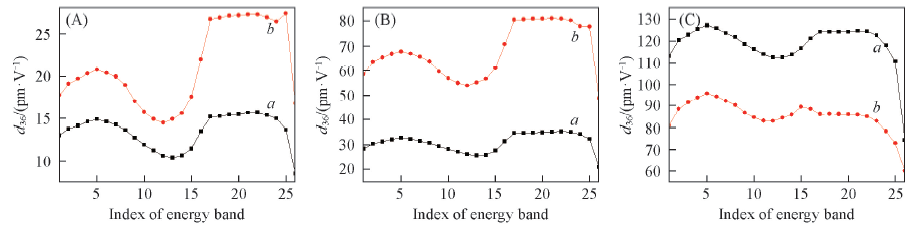
Fig.8 Variations of d36 coefficient as a function of the numbers of occupied bands of CuGaS2(a) and CuInS2(b)(A), CuGaSe2(a) and CuInSe2(b)(B), CuGaTe2(a) and CuInTe2(b)(C) crystalsThe index of HOCO is 26, and the d36 magnitude is obtained by considering a total of 34 unoccupied energy bands.

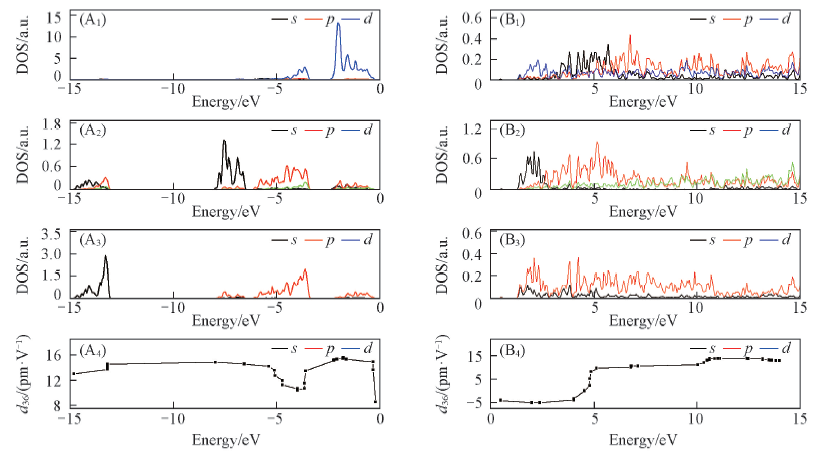
Fig.9 Variations of HOCO band component of CuXY2 at the k point of [0.4,0.2,0] (A) Cu; (B) X; (C) Y.

Fig.10 Correlations between d36 coefficients and the occupied(A1—A4)/ unoccupied(B1—B4) DOSs of CuGaS2 crystals(A1, B1) Cu; (A2, B2) Ga; (A3, B3) S; (A4, B4) d36. The zero energy is set to EF, and the d36 magnitude at a certain energy level(E) is obtained by considering all the occupied/unoccupied bands distributed in the region between E and EF.

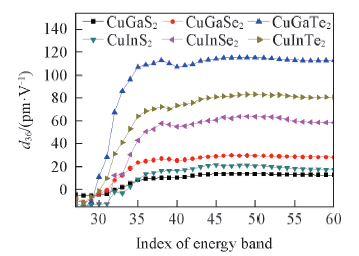
Fig.11 Variations of d36 coefficient as a function of the numbers of unoccupied bands of CuXY2The index of the LUCO is 27, and the d36 magnitude is obtained by considering a total of 26 occupied energy bands.

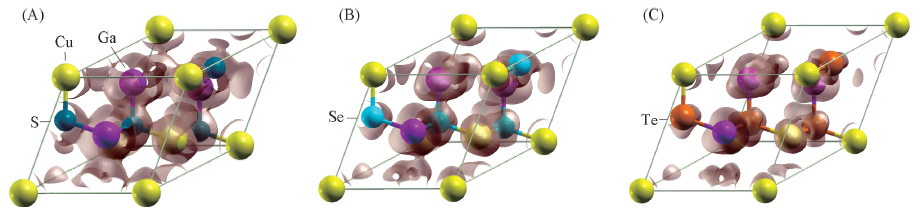
Fig.12 3D charge density maps of unoccupied bands from the 32nd to 36th of CuGaY2(A) CuGaS2; (B) CuGaSe2; (C) CuGaTe2. The corresponding isovalue is 6.0 e/nm3.

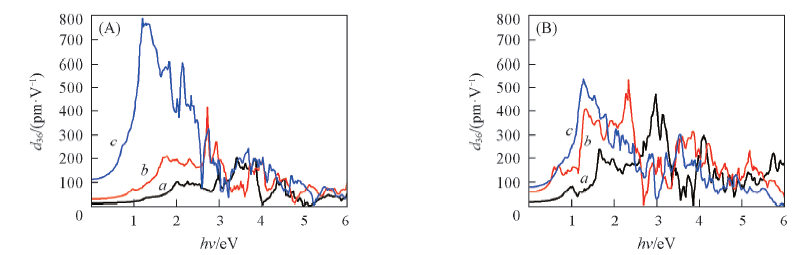
Fig.13 Frequency-dependent variations of the d36 coefficients of CuGaY2(A) and CuInY2(B) crystals (A) a. CuGaS2; b. CuGaSe2; c. CuGaTe2. (B) a. CuInS2; b. CuInSe2; c. CuInTe2.

参考文献 40

[1]	Verozubova G. A., Gribenyukov A. I., Korotkova V. V., Semchinova O., Uffmann D., J. Cryst. Growth, 2000, 213, 334—339
[2]	Bai L., Lin Z.S.., Wang Z. Z., Chen C. T., Lee M. H.,J. Chem. Phys., 2004, 120, 8772—8778
[3]	Chen C. T., Bai L., Wang Z. Z., Li R. K., J. Cryst. Growth, 2006, 292, 169—17
[4]	Shimizu A., Chaisitsak S., Sugiyama T., Yamada A., Konagai M., Thin Solid Films, 2000, 361, 193—197
[5]	Mitchell K. W., Eberspacher C., Ermer J. H., Pauls K. L., Pier D. N., Ieee Transactions on Electron Devices, 1990, 37, 410—417
[6]	Hwang H. L., Chang H. H., Sharma P., Letha A. J., Shao L. X., Zhang Y. F., Tseng B. H., Adv. Sci., 2016, 3, 1500196
[7]	Aissaoui O., Mehdaoui S., Bechiri L., Benabdeslem M., Benslim N., Amara A., Mahdjoubi L., Nouet G., J. Phys. D-Appl. Phys., 2007, 40, 5663—5665
[8]	Zhu S. F., Zhao B. J., Liu J., Li Z. H., Li W. T., Mater. Chem. Phys., 1997, 50, 94—97
[9]	Singh N.B.., Hopkins R. H., Feichtner J. D.,J. Mater. Sci., 1986, 21, 837—841
[10]	Badikov V. V., Laptev V. B., Panyutin V. L., Ryabov E. A., Shevyrdyaeva G. S., Shcherbina O. B., Kvantovaya Elektron, 1992, 19, 782—784
[11]	Verma A. S., Physica Status Solidi B-Basic Solid State Physics, 2009, 246, 345—353
[12]	Arai S., Ozaki S., Adachi S., Appl. Optics., 2010, 49, 829—837
[13]	Ouahrani T., Otero-de-la-Roza A., Reshak A. H., Khenata R., Faraoun H. I., Amrani B., Mebrouki M., Luana V., Phys. B, 2010, 405, 3658—3664
[14]	Chen S. Y., Gong X. G., Wei S. H., Phys. Rev. B, 2007, 75, 205209
[15]	Rashkeev S. N., Lambrecht W. R. L., Phys. Rev. B, 2001, 63, 165212
[16]	Ghosh A., Thangavel R., Rajagopalan M., J. Mater. Sci., 2015, 50, 1710—1717
[17]	Perdew J. P., Chevary J. A., Vosko S. H., Jackson K. A., Pederson M. R., Singh D. J., Fiolhais C., Phys. Rev. B, 1992, 46, 6671—6687
[18]	Liang D. M., Leng X., Ma Y. C., Chem. Res. Chinese Universities, 2016, 32(6), 996—1004
[19]	Yan L. L., Liu C. G., Jiang M. X., Chem. J. Chinese Universities, 2019, 39(5), 1034—1040
	(严玲玲, 刘春光, 蒋梦绪. 高等学校化学学报, 2019, 39(5), 1034—1040)
[20]	Xiao H., Tahir-Kheli J., Goddard W. A., J. Phys. Chem. Lett., 2011, 2, 212—217
[21]	Rashkeev S. N., Lambrecht W. R. L., Segall B., Phys. Rev. B, 1998, 57, 3905—3919
[22]	Ni B. L., Zhou H. G., Jiang J. Q., Li Y., Zhang Y. F., Acta Phys. Chim. Sin., 2010, 26, 3052—3260
	(倪碧莲, 周和根, 姜俊全, 李奕, 章永凡. 物理化学学报, 2010, 26, 3052—3060)
[23]	Chen D., Xiao H. Y., Jia W., Chen H., Zhou H. G., Li Y., Ding K. N., Zhang Y. F., Acta Phys. Sin., 2012, 61, 127103
	(陈懂, 肖河阳, 加伟, 陈虹, 周和根, 李奕, 丁开宁, 章永凡. 物理学报, 2012, 61, 127103)
[24]	Fang Z. X., Lin J., Liu R., Liu P., Li Y., Huang X., Ding K. N., Ning L. X., Zhang Y. F., Cryst. Eng. Comm., 2014, 16, 10569—10580
[25]	Godby R. W., Schluter M., Sham L. J., Phys. Rev. B, 1988, 37, 10159—10175
[26]	Kresse G., Furthmuller J., Comp. Mater. Sci., 1996, 6, 15—50
[27]	Kresse G., Furthmuller J., Phys. Rev. B, 1996, 54, 11169—11186
[28]	Huang Y.Z.., Wu L. M., Wu X. T., Li L. H., Chen L., Zhang Y. F.,J. Am. Chem. Soc., 2010, 132, 12788—12789
[29]	Lin J., Fang Z. X., Tao H. L., Li Y., Huang X., Ding K. N., Huang S. P., Zhang Y. F., Cryst. Eng. Comm., 2019, 20, 2573—2582
[30]	Zhou H. G., Wen X. W., Fang Z. X., Li Y., Ding K. N., Huang X., Zhang Y. F., Acta Phys. Chim. Sin., 2013, 29(5), 920—928
	(周和根, 温兴伟, 方振兴, 李奕, 丁开宁, 黄昕, 章永凡. 物理化学学报, 2013, 29(5), 920—928)
[31]	Mandel L., Tomlinson R.D.., Hampshire M. J.,J. Appl. Crystallogr., 1973, 10, 130—131
[32]	Leon M., Merino J. M., Devidales J. L. M., Journal of Vacuum Science & Technology a-Vacuum Surfaces and Films, 1993, 11, 2430—2436
[33]	Hussain K. M. A., Podder J., Saha D. K., Ichimura M., Indian J. Pure Ap. Phy., 2012, 50, 117—122
[34]	Gladkikh L. I., Rogacheva E. I., Tavrina T. V., Fomina L. P., Inorg. Mater., 2000, 36, 1098—1100
[35]	Knight K. S., Mater. Res. Bull., 1992, 27, 161—167
[36]	Nayebi P., Mirabbaszadeh K., Shamshirsaz M., Phys. B, 2013, 416, 55—63
[37]	Davis J.G.., Bridenbaugh P. M., Wagner S.,J. Electro. Mater., 1978, 7, 39—45
[38]	Alonso M. I., Wakita K., Pascual J., Garriga M., Yamamoto N., Phys. Rev. B, 2001, 63, 075203
[39]	Levcenko S., Syrbu N. N., Tezlevan V. E., Arushanov E., Doka-Yamigno S., Schedel-Niedrig T., Lux-Steiner M. C., J. Phys. Condens. Matter, 2007, 19, 456222
[40]	WeberJ. M., Handbook of Optical Materials, CRC Press, Boca Raton, 2003, 218