

高等学校化学学报 ›› 2021, Vol. 42 ›› Issue (7): 2085.doi: 10.7503/cjcu20210151
收稿日期:2021-03-08
出版日期:2021-07-10
发布日期:2021-04-16
通讯作者:
帅志刚
E-mail:zgshuai@tsinghua.edu.cn
基金资助:
LI Weitang, REN Jiajun, SHUAI Zhigang( )
)
Received:2021-03-08
Online:2021-07-10
Published:2021-04-16
Contact:
SHUAI Zhigang
E-mail:zgshuai@tsinghua.edu.cn
Supported by:摘要:
密度矩阵重正化群(DMRG)作为计算低维强关联体系强有力的方法为人熟知, 在量子化学电子结构计算中得到广泛应用. 最近几年, 含时密度矩阵重正化群(TD-DMRG)的理论取得较快发展, TD-DMRG逐渐成为复杂体系量子动力学理论模拟的重要新兴方法之一. 本文综述了基于矩阵乘积态(MPS) 和矩阵乘积算符(MPO)的DMRG基本理论, 并重点介绍了若干最常见的TD-DMRG时间演化算法, 包括基于演化再压缩(P&C) 的算法、 基于含时变分原理(TDVP)的算法和时间步瞄准(TST)算法; 还对利用TD-DMRG模拟有限温体系的纯化(Purification)算法和最小纠缠典型量子热态(METTS)算法进行了介绍. 最后, 对近年TD-DMRG在复杂体系量子动力学中的应用进行了总结.
中图分类号:
TrendMD:
李维唐, 任佳骏, 帅志刚. 含时密度矩阵重正化群的理论与应用. 高等学校化学学报, 2021, 42(7): 2085.
LI Weitang, REN Jiajun, SHUAI Zhigang. Theory and Applications of Time Dependent Density Matrix Renormalization Group. Chem. J. Chinese Universities, 2021, 42(7): 2085.
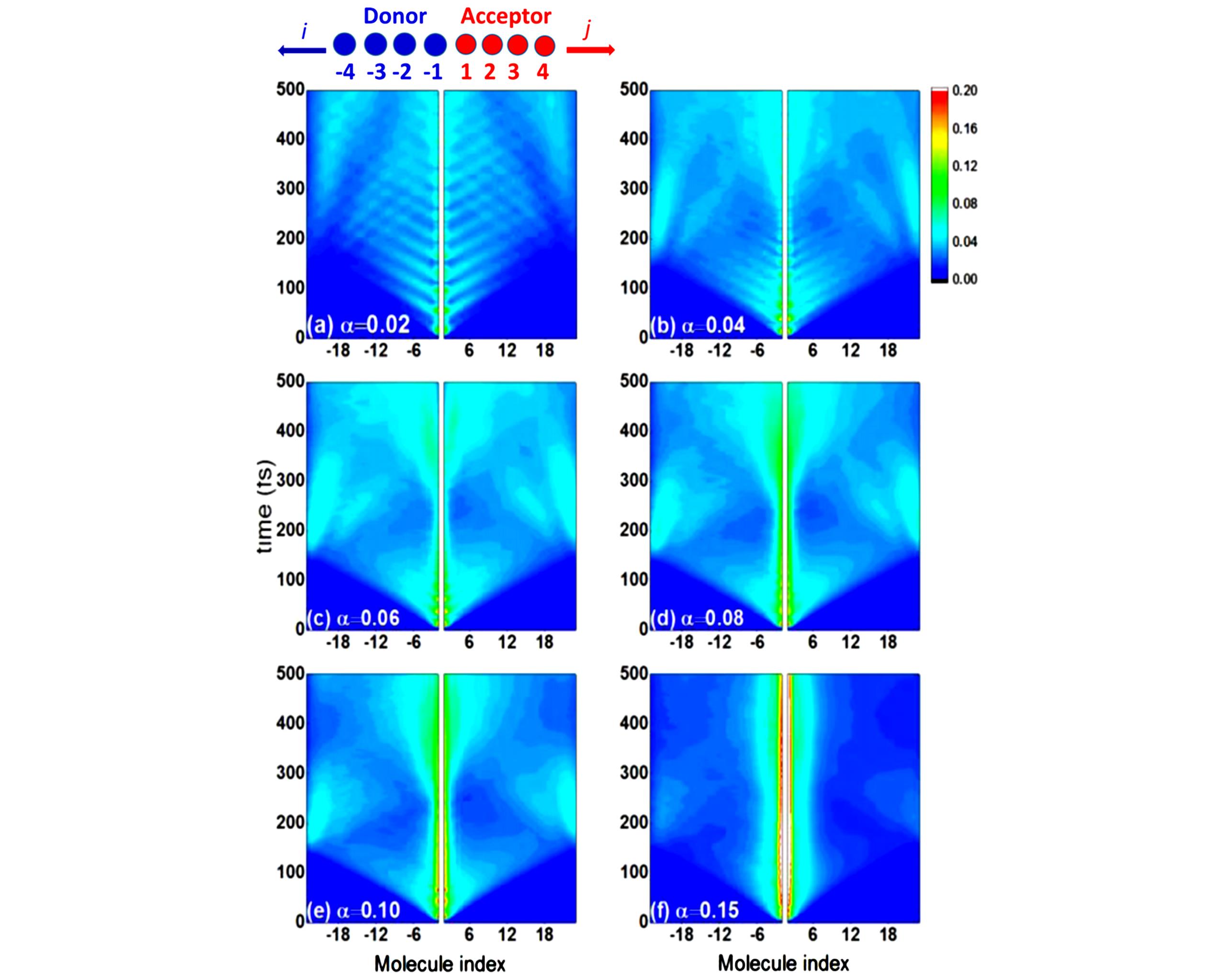
Fig.4 Charge density evolution of hole in the donor part and electron in the acceptor part with different α values[21]α is the electron?phonon coupling strength. Copyright 2016, American Chemical Society.
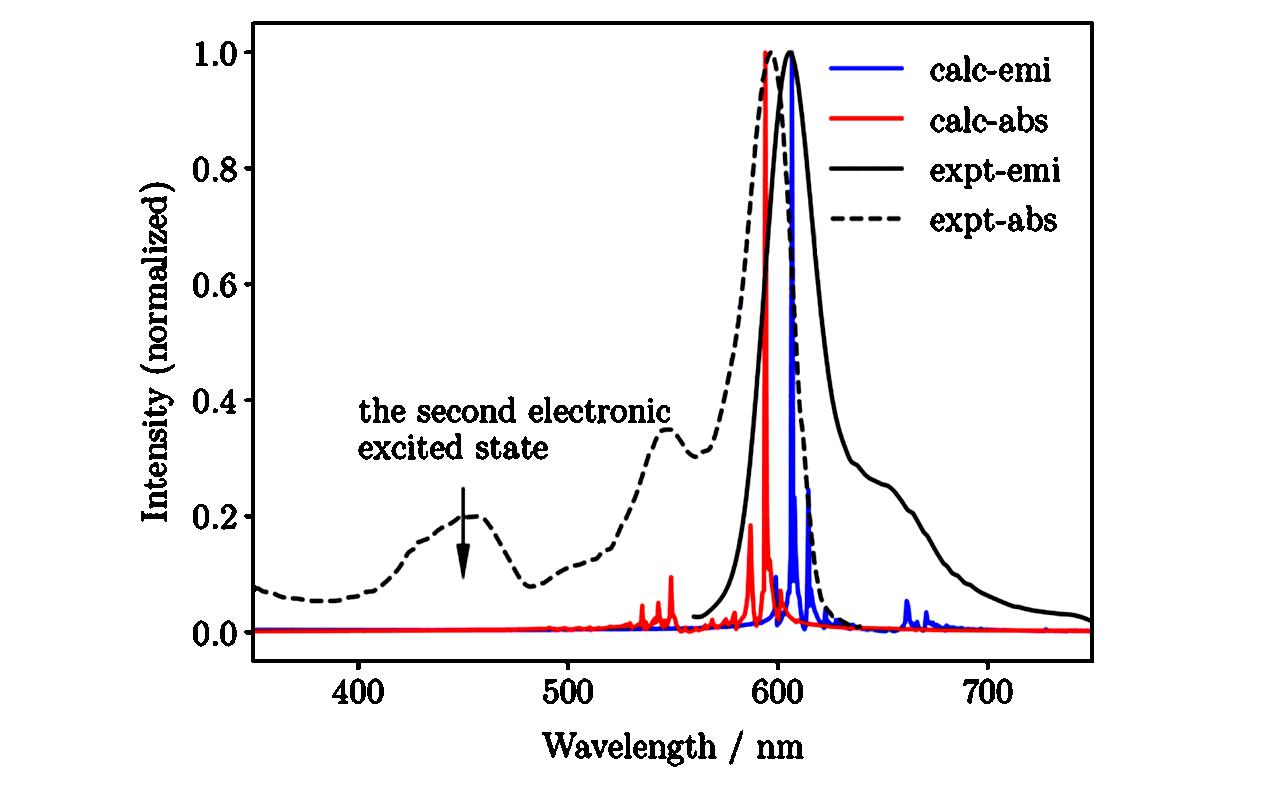
Fig.5 Calculated absorption and fluorescence spectra of PBI dimer at 298 K from finite temperature TD?DMRG[23]Copyright 2018, American Chemical Society.
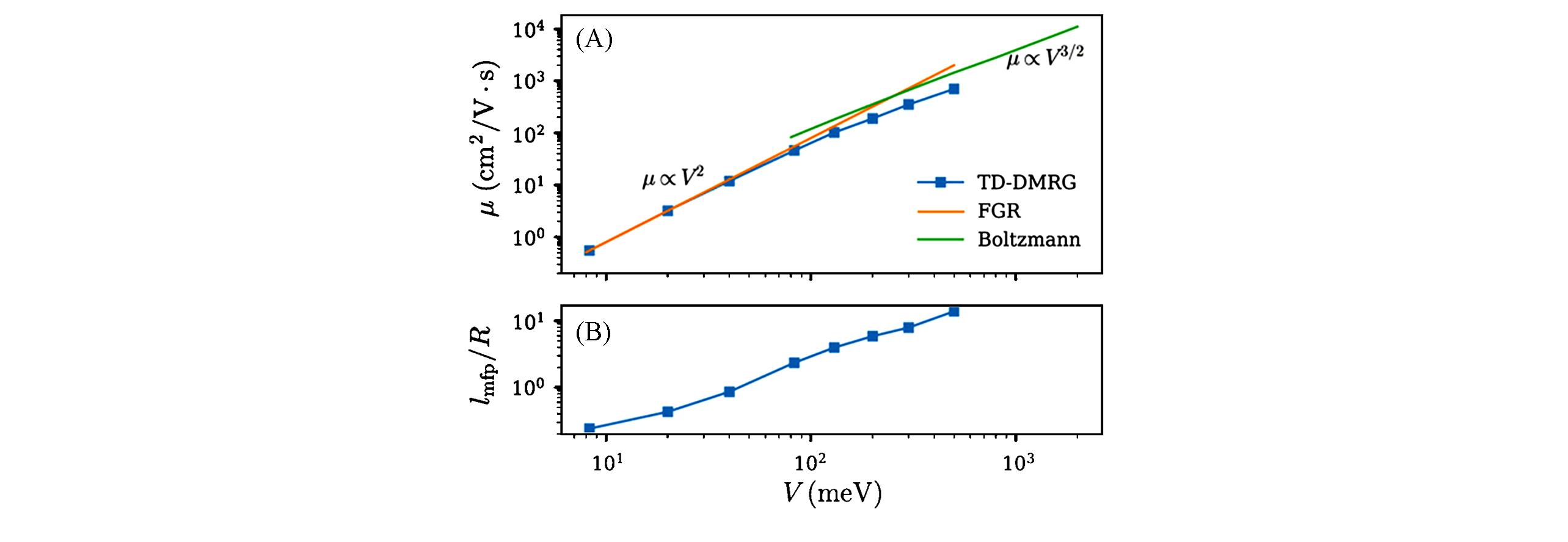
Fig.6 Carrier mobility from weak to strong electronic coupling(V) calculated by TD?DMRG, FGR(hopping limit), and Boltzmann transport theory(band limit)(A), mean free path(lmfp) of the charge carrier from weak to strong electronic coupling calculated by TD?DMRG(B)[25]In both panels the electron?phonon coupling parameters are adopted from the first?principle calculation of rubrene crystal. Copyright 2020, American Chemical Society.
| 1 | White S. R., Phys. Rev. Lett., 1992, 69, 2863 |
| 2 | White S. R., Phys. Rev. B, 1993, 48, 10345 |
| 3 | Shuai Z., Brédas J. L., Pati S. K., Ramasesha S., Proc. SPIE, 1997, 3145,293—302 |
| 4 | Shuai Z., Brédas J. L., Pati S. K., Ramasesha S., Phys. Rev. B, 1997, 56, 9298—9301 |
| 5 | Shuai Z., Brédas J. L., Saxena A., Bishop A. R., J. Chem. Phys., 1998, 109(6), 2549—2555 |
| 6 | Fano G., Ortolani F., Ziosi L., J. Chem. Phys., 1998, 108(22), 9246—9252 |
| 7 | White S. R., Martin R. L., J. Chem. Phys., 1999, 110(9), 4127—4130 |
| 8 | Chan G. K. L., Head⁃Gordon M., J. Chem. Phys., 2002, 116(11), 4462—4476 |
| 9 | Moritz G., Wolf A., Reiher M., J. Chem. Phys., 2005, 123(18), 184105 |
| 10 | Chan G. K. L., van Voorhis T., J. Chem. Phys., 2005, 122(20), 204101 |
| 11 | Kurashige Y., Yanai T., J. Chem. Phys., 2009, 130(23), 234114 |
| 12 | Cazalilla M., Marston J., Phys. Rev. Lett., 2002, 88, 256403 |
| 13 | Luo H., Xiang T., Wang X., Phys. Rev.Lett., 2003, 91, 049701 |
| 14 | White S. R., Feiguin A. E., Phys. Rev. Lett., 2004, 93, 076401 |
| 15 | Feiguin A. E., White S. R., Phys. Rev. B, 2005, 72(2), 020404 |
| 16 | Schollwöck U., Ann. Phys., 2011, 326(1), 96—192 |
| 17 | Paeckel S., Köhler T., Swoboda A., Manmana S. R., Schollwöck U., Hubig C., Ann. Phys., 2019, 411, 167998 |
| 18 | García⁃Ripoll J. J., New J. Phys., 2006, 8(12), 305 |
| 19 | Haegeman J., Cirac J. I., Osborne T. J., Pižorn I., Verschelde H., Verstraete F., Phys. Rev. Lett., 2011, 107(7), 070601 |
| 20 | Haegeman J., Lubich C., Oseledets I., Vandereycken B., Verstraete F., Phys. Rev. B, 2016, 94(16), 165116 |
| 21 | Yao Y., Xie X., Ma H., J. Phys. Chem. Lett., 2016, 7(23), 4830—4835 |
| 22 | Yao Y., Sun K. W., Luo Z., Ma H., J. Phys.Chem. Lett., 2018, 9(2), 413—419 |
| 23 | Ren J., Shuai Z., Chan G. K., J. Chem. Theory Comput., 2018, 14, 5027—5039 |
| 24 | Baiardi A., Reiher M., J. Chem. Theory Comput., 2019, 15(6), 3481—3498 |
| 25 | Li W., Ren J., Shuai Z., J. Phys. Chem. Lett., 2020, 11(13), 4930—4936 |
| 26 | Yarkony D. R., Chem. Rev., 2012, 112(1), 481—498 |
| 27 | Crespo⁃Otero R., Barbatti M., Chem. Rev., 2018, 118(15), 7026—7068 |
| 28 | Meyer H. D., Manthe U., Cederbaum L., Chem. Phys. Lett., 1990, 165(1), 73—78 |
| 29 | Beck M. H., Jäckle A., Worth G. A., Meyer H. D., Phys. Rep., 2000, 324(1), 1—105 |
| 30 | Wang H., Thoss M., J. Chem. Phys., 2003, 119(3), 1289—1299 |
| 31 | Wang H., J. Phys. Chem. A, 2015, 119(29), 7951—7965 |
| 32 | Tully J. C., J. Chem. Phys., 1990, 93(2), 1061—1071 |
| 33 | Wang L., Qiu J., Bai X., Xu J., Wiley Interdiscip. Rev. Comput. Mol. Sci., 2020, 10(2), e1435 |
| 34 | Grasedyck L., SIAM J. Matrix Anal. Appl., 2010, 31(4), 2029—2054 |
| 35 | Kloss B., Burghardt I., Lubich C., J. Chem. Phys., 2017, 146(17), 174107 |
| 36 | Kurashige Y., J. Chem. Phys., 2018, 149(19), 194114 |
| 37 | Li W., Ren J., Shuai Z., J. Chem. Phys., 2020, 152(2), 024127 |
| 38 | Ronca E., Li Z., Jimenez⁃Hoyos C. A., Chan G. K. L., J. Chem.Theory Comput., 2017, 13(11), 5560—5571 |
| 39 | Frahm L. H., Pfannkuche D., J.Chem. Theory Comput., 2019, 15(4), 2154—2165 |
| 40 | Ma H., Luo Z., Yao Y., Mol. Phys., 2018, 116(7/8), 854—868 |
| 41 | Chan G. K. L., Keselman A., Nakatani N., Li Z., White S. R., J. Chem. Phys., 2016, 145(1), 014102 |
| 42 | Vidal G., Phys. Rev. Lett., 2004, 93, 040502 |
| 43 | Daley A. J., Kollath C., Schollwöck U., Vidal G., J. Stat. Mech.: Theory Exp., 2004, 2004(4), P04005 |
| 44 | Zaletel M. P., Mong R. S., Karrasch C., Moore J. E., Pollmann F., Phys. Rev. B, 2015, 91(16), 165112 |
| 45 | Wall M. L., Carr L. D., New J. Phys., 2012, 14(12), 125015 |
| 46 | Halimeh J. C., Kolley F., McCulloch I. P., Phys. Rev. B, 2015, 92, 115130 |
| 47 | Greene S. M., Batista V. S., J. Chem. Theory Comput., 2017, 13(9), 4034— 4042 |
| 48 | Dirac P. A. M., Math. Proc. Camb. Philos. Soc., 1930, 26(3), 376—385 |
| 49 | Dutta T., Ramasesha S., Phys. Rev. B, 2010, 82(3), 035115 |
| 50 | Borrelli R., Gelin M. F., Sci. Rep., 2017, 7, 9127 |
| 51 | Xie X., Liu Y., Yao Y., Schollwöck U., Liu C., Ma H., J. Chem. Phys., 2019, 151(22), 224101 |
| 52 | Kloss B., Reichman D. R., Tempelaar R., Phys. Rev. Lett., 2019, 123, 126601 |
| 53 | Stoudenmire E. M., White S. R., New. J. Phys., 2010, 12(5), 055026 |
| 54 | Prior J., Chin A. W., Huelga S. F., Plenio M. B., Phys. Rev. Lett., 2010, 105(5), 050404 |
| 55 | Ma H., Schollwöck U., J. Chem. Phys., 2008, 129(24), 244705 |
| 56 | Chin A. W., Prior J., Rosenbach R., Caycedo⁃Soler F., Huelga S., Plenio M., Nat. Phys., 2013, 9, 113—118 |
| 57 | Mannouch J. R., Barford W., Al⁃Assam S., J. Chem. Phys., 2018, 148(3), 034901 |
| 58 | Gatti F., Lasorne B., Meyer H. D., Nauts A., Applications of Quantum Dynamics in Chemistry, Vol. 98, Springer, New York, 2017 |
| 59 | Wouters S., Nakatani N., van Neck D., Chan G. K. L., Phys. Rev. B, 2013, 88(7), 075122 |
| 60 | Meyer H. D., Wang H., J. Chem. Phys., 2018, 148(12), 124105 |
| 61 | Wang H., Meyer H. D., J. Chem. Phys., 2018, 149(4), 044119 |
| 62 | Lubich C., Oseledets I., Vandereycken B., SIAM J. Numer. Anal., 2015, 53(2), 917—941 |
| 63 | Verstraete F., Garcia⁃Ripoll J. J., Cirac J. I., Phys. Rev. Lett., 2004, 93(20), 207204 |
| 64 | Feiguin A. E., White S. R., Phys. Rev. B, 2005, 72(22), 220401 |
| 65 | White S. R., Phys. Rev. Lett., 2009, 102, 190601 |
| 66 | Chen J., Stoudenmire E. M., Phys. Rev. B, 2020, 101, 195119 |
| 67 | Takahashi Y., Umezawa H., Int. J. Mod. Phys. A, 1996, 10(13/14), 1755—1805 |
| 68 | De Vega I., Bañuls M. C., Phys. Rev. A, 2015, 92, 052116 |
| 69 | Borrelli R., Gelin M. F., J. Chem. Phys., 2016, 145(22), 224101 |
| 70 | Tamascelli D., Smirne A., Lim J., Huelga S. F., Plenio M. B., Phys. Rev. Lett., 2019, 123, 090402 |
| 71 | Borrelli R., Chem. Phys., 2018, 515, 236—241 |
| 72 | Gelin M. F., Borrelli R., Domcke W., J. Phys. Chem. Lett., 2019, 10(11), 2806—2810 |
| 73 | Barford W., Mannouch J. R., J. Chem. Phys., 2018, 149(21), 214107 |
| 74 | Yao Y., Phys. Rev. B, 2016, 93, 115426 |
| 75 | Worth G. A., Meyer H., Cederbaum L. S., J. Chem. Phys., 1996, 105(11), 4412—4426 |
| 76 | Raab A., Worth G. A., Meyer H. D., Cederbaum L. S., J. Chem. Phys., 1999, 110(2), 936—946 |
| 77 | Zhao D., Silva R. E. F., Climent C., Feist J., Fernández⁃Domínguez A. I., García⁃Vidal F. J., ACS Photonics, 2020, 7(12), 3369—3375 |
| 78 | Ma H., Schollwöck U., J. Phys. Chem. A, 2009, 113(7), 1360—1367 |
| 79 | Zhao H., Yao Y., An Z., Wu C. Q., Phys. Rev. B, 2008, 78, 035209 |
| 80 | Ren J., Li W., Jiang T., Shuai Z., J. Chem. Phys., 2020, 153(8), 084118 |
| 81 | Calabrese P., Cardy J., J. Stat.Mech., 2005, 2005(4), P04010 |
| 82 | Žnidarič M., Commun. Phys., 2020, 3(1), 100 |
| 83 | Jiang T., Ren J. J., Shuai Z. G., Chem. J. Chinese Universities, 2020, 41(12), 2610—2628(姜童, 任佳骏, 帅志刚. 高等学校化学学报, 2020, 41(12), 2610—2628) |
| 84 | Rams M. M., Zwolak M., Phys. Rev. Lett., 2020, 124, 137701 |
| [1] | 安丰, 胡茜茜, 谢代前. 三原子分子非绝热传能动力学的研究进展[J]. 高等学校化学学报, 2021, 42(7): 2103. |
| [2] | 边文生, 曹剑炜. PBFC-PI量子动力学方法及应用[J]. 高等学校化学学报, 2021, 42(7): 2123. |
| [3] | 贺进禄, 龙闰, 方维海. 非绝热分子动力学模拟A位阳离子对钙钛矿热载流子弛豫的影响[J]. 高等学校化学学报, 2020, 41(3): 439. |
| [4] | 姜童, 任佳骏, 帅志刚. 频域空间密度矩阵重正化群的研究进展[J]. 高等学校化学学报, 2020, 41(12): 2610. |
| [5] | 胡茜茜, 杨俊英, 谢代前. 反应N+NH→N2+H的态-态量子动力学研究[J]. 高等学校化学学报, 2015, 36(11): 2198. |
| [6] | 欧阳冰, 薛佳丹, 郑旭明. γ-巴豆酰内酯激发态动力学的共振拉曼光谱和完全活性空间自洽场(CASSCF)计算研究[J]. 高等学校化学学报, 2015, 36(10): 1995. |
| 阅读次数 | ||||||
|
全文 |
|
|||||
|
摘要 |
|
|||||