频域空间密度矩阵重正化群的研究进展

doi:10.7503/cjcu20200767

摘要/Abstract

摘要：

密度矩阵重正化群(DMRG)作为低维强关联体系中电子结构计算的强有力方法被广泛熟知, 并被迅速地应用于量子化学, 不仅在电子结构计算中发挥重要作用, 同时也在近几年迅速地成为复杂体系量子动力学计算的重要方法. 在DMRG框架中, 衍生出了一系列计算动态响应性质的有效方法, 并得到了广泛应用. 本文简述了DMRG的基本理论, 其矩阵乘积态(MPS)表示有效地扩展了该方法的应用范围. 重点介绍了基于线性响应理论的动态DMRG, 在频率空间求解系统在零温以及有限温度下响应性质的算法, 并介绍其在电子关联问题和电子-声子关联问题中的应用, 最后展望了该领域的未来发展方向.

关键词: 密度矩阵重正化群, 矩阵乘积态, 线性响应性质, 分子聚集体, 电子-声子耦合

Abstract:

Density matrix renormalization group（DMRG） has been developed for electron correlation in low-dimensional system and has been quickly applied to quantum chemistry as a powerful method for electronic structure calculation and for quantum dynamics of complex system. After more than 20 years of development， a series of effective methods for calculating dynamic response properties within DMRG have been developed and have been extensively applied for spectroscopy. We will first briefly describe the main features of DMRG， including its matrix product state（MPS） formulation. Based on the linear response theory， we focus on descri-bing the DMRG algorithms in frequency domain to solve the response properties both for zero temperature and finite temperature. We then introduce several most relevant applications in electronic correlation problems and electron-phonon correlation problems.

Key words: Density matrix renormalization group（DMRG）, Matrix product state, Linear response property, Molecular aggregate, Electron-phonon coupling（Ed.： Y, K, S）

中图分类号:

O649

TrendMD:

姜童, 任佳骏, 帅志刚. 频域空间密度矩阵重正化群的研究进展. 高等学校化学学报, 2020, 41(12): 2610.

JIANG Tong, REN Jiajun, SHUAI Zhigang. Frequency Domain Density Matrix Renormalization Group. Chem. J. Chinese Universities, 2020, 41(12): 2610.

图/表 21

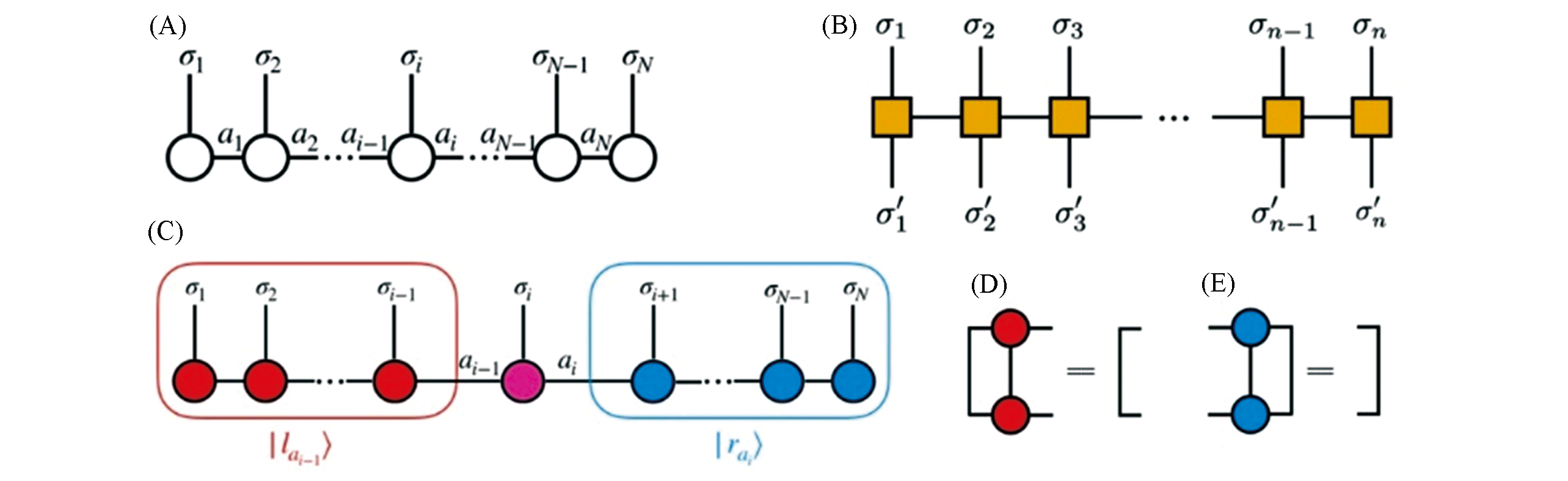
Fig.1 Graphical representation of matrix product state/operator(MPS/MPO) of wavefunction and operator(A) General wavefunction represented with MPS; (B) operator represented with MPO; (C) mixed?canonical MPS representation of wavefunction, the pink circle is Cσi, matrices to the left is left?normalized(D), to the right is right?normalized(E).

Fig.2 Adding two different MPOs

Fig.3 Applying an MPO to an MPS

Fig.4 Overlaps and expectation values

Fig.5 Eigenvalue problem when minimizing the Lagrangian with respect to local matrix Cσi

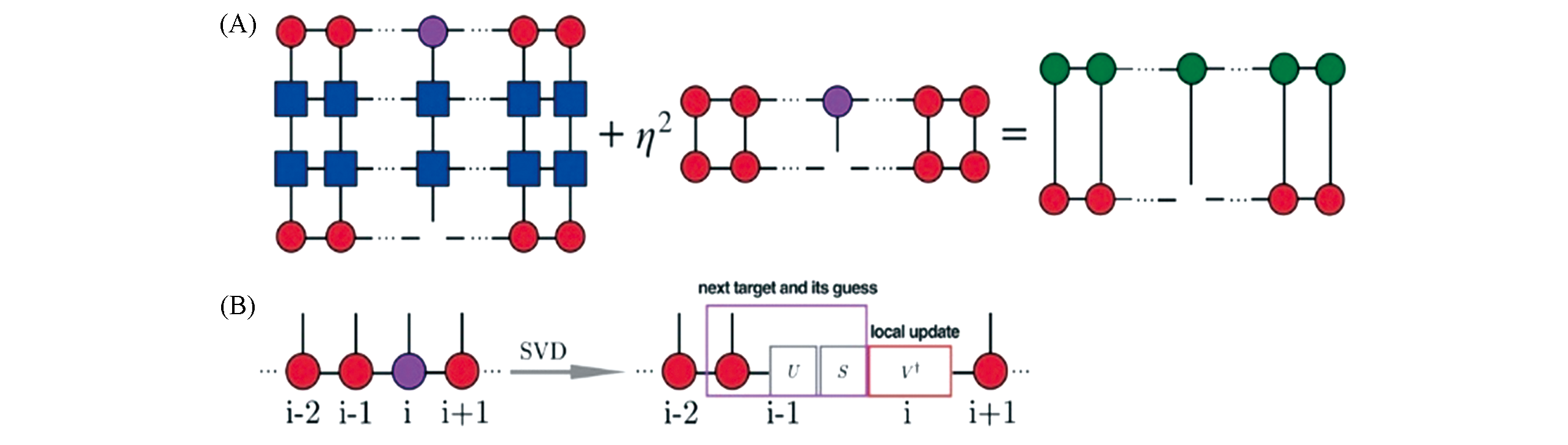
Fig.6 Graphical representation of minimizing the Lagrangian with respect to local matrix Aσi[22](A) Linear equation problem of optimizing Aσi, Aσi is marked in purple; (B) when sweep to left, Singular value decomposition(SVD) of Aσi each time after solving the local linear equation and update the local site Aσi and meanwhile obtain the guess for Aσi-1. Copyright 2020, American Chemical Society.

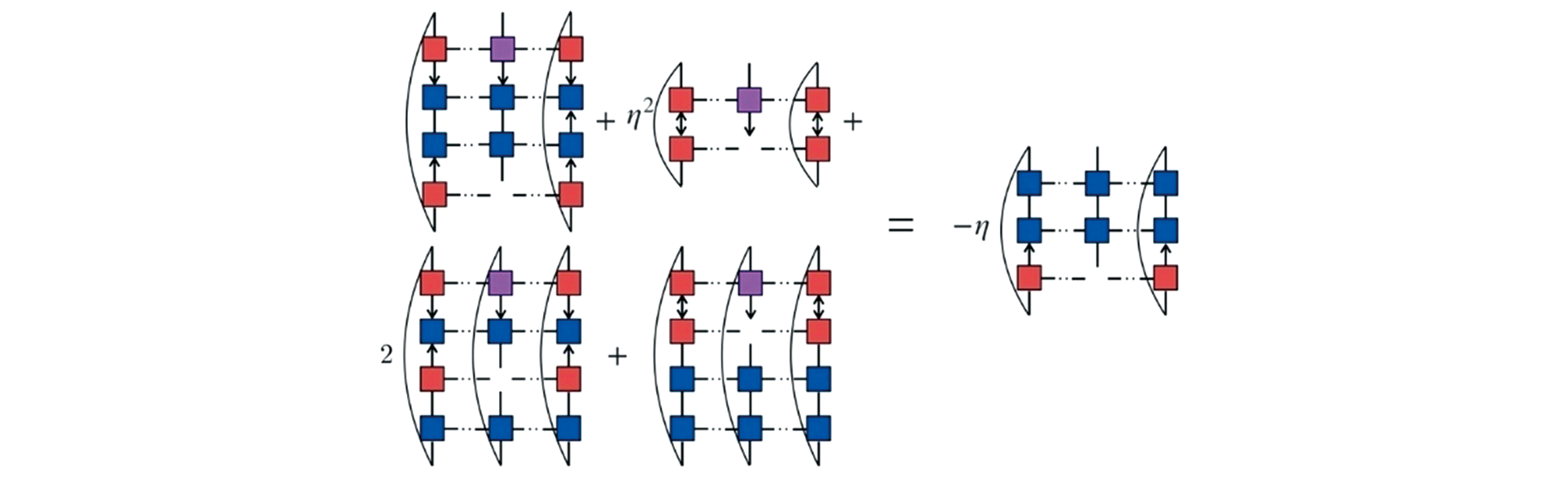
Fig.7 Graphical representation of obtaining the ensemble expectation value of operator(marked in blue) by thermal field dynamics

Fig.8 Linear equation ?F/?Aσi=0(Eq.55) to optimize the local site Aσi(in purple) at finite temperature[22]Aσj(j≠i) is marked in red. The operators ω-H?0, H?0, μ?, ρβ1/2 are shown in blue.Copyright 2020, American Chemical Society.

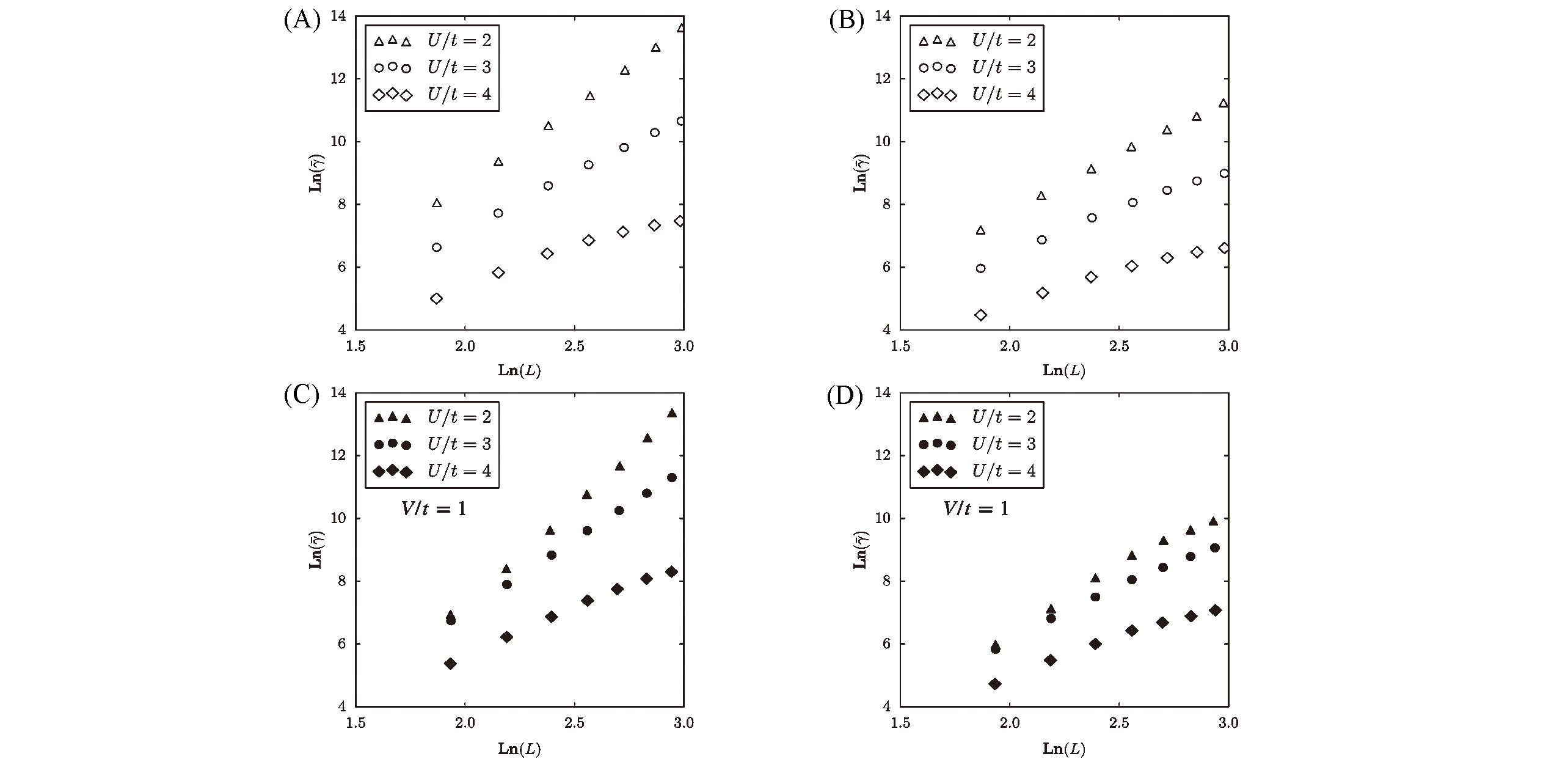
Fig.9 Representation of extended Hubbard?Peierls model

Fig.10 Plot of the log of average third?order polarizability γˉvs. log of the chain length L[8]Hubbard chain with three different values of U/t for δ=0(A) and δ=0.09(B); Hubbard?Peierls chain with three different values of U/t?and V/t=1 for δ=0(C) and δ=0.09(D).Copyright 1999, American Physical Society.

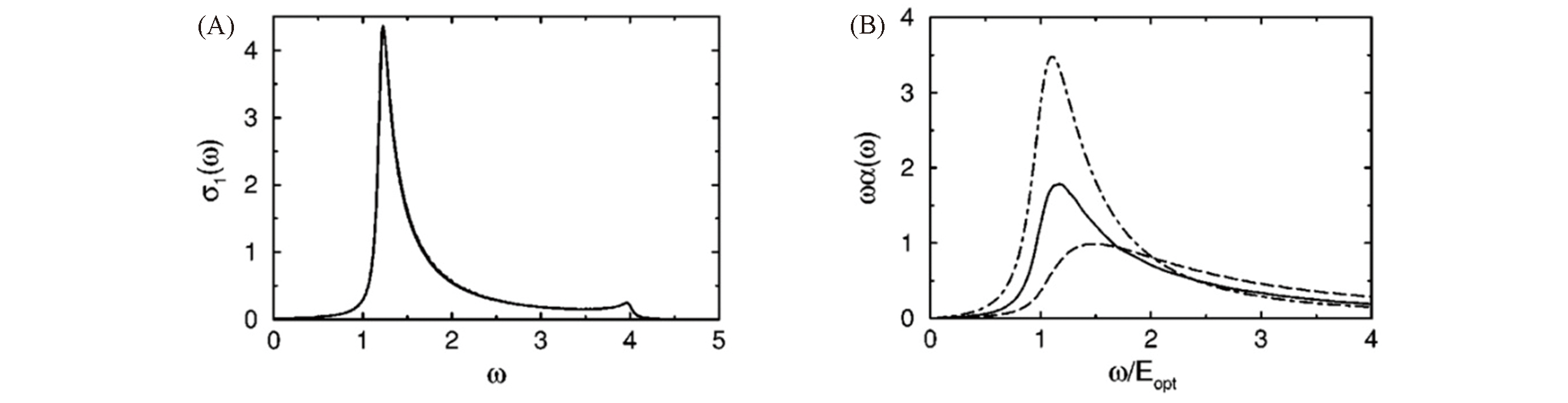
Fig.11 Optical conductivity calculated by DDMRG[21](A) Peierls insulator with U=0 and δ=0.3, both DDMRG result for a 128?site chain and the exact result in the thermodynamic limit are shown(broadening width η=0.05t); (B) optical conductivity on a 128?site chain for: Mott?Hubbard insulator with U=3t, δ=0(dashed), Peierls insulator with U=0, δ=0.15(dot dashed), and Hubbard?Peierls insulator with U=2.3t, δ=0.075(solid), broadening width η=0.1t.Copyright 2002, American Physical Society.

Fig.12 Dependence ofthe local density of states at the central site of a hydrogen chain(N=10) with different bond dimensions[14]A broadening(η) of 0.005 a.u. has been used. (A) DDMRG result, (B) TD?DMRG result.Copyright 2017, American Chemical Society.

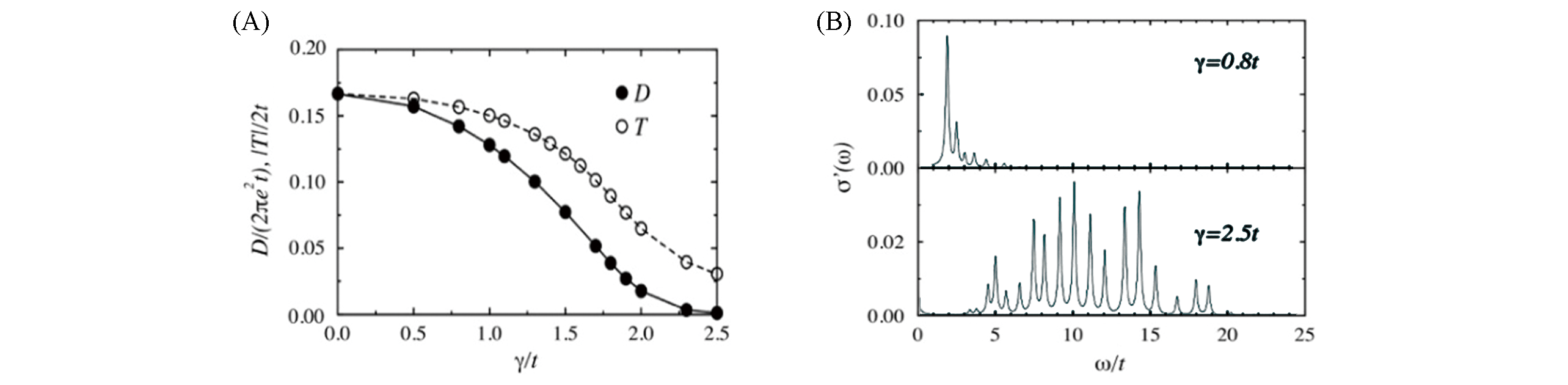
Fig.13 Dynamical properties of Holstein model[43](A) Drude weight D and the kinetic energy per site T as a function of the electron?phonon coupling γ; (B) the incoherent part of the optical conductivity σ'ω? in the quasi?free electron regime(γ=0.3t) and in the small polaron regime(γ=2.5t).

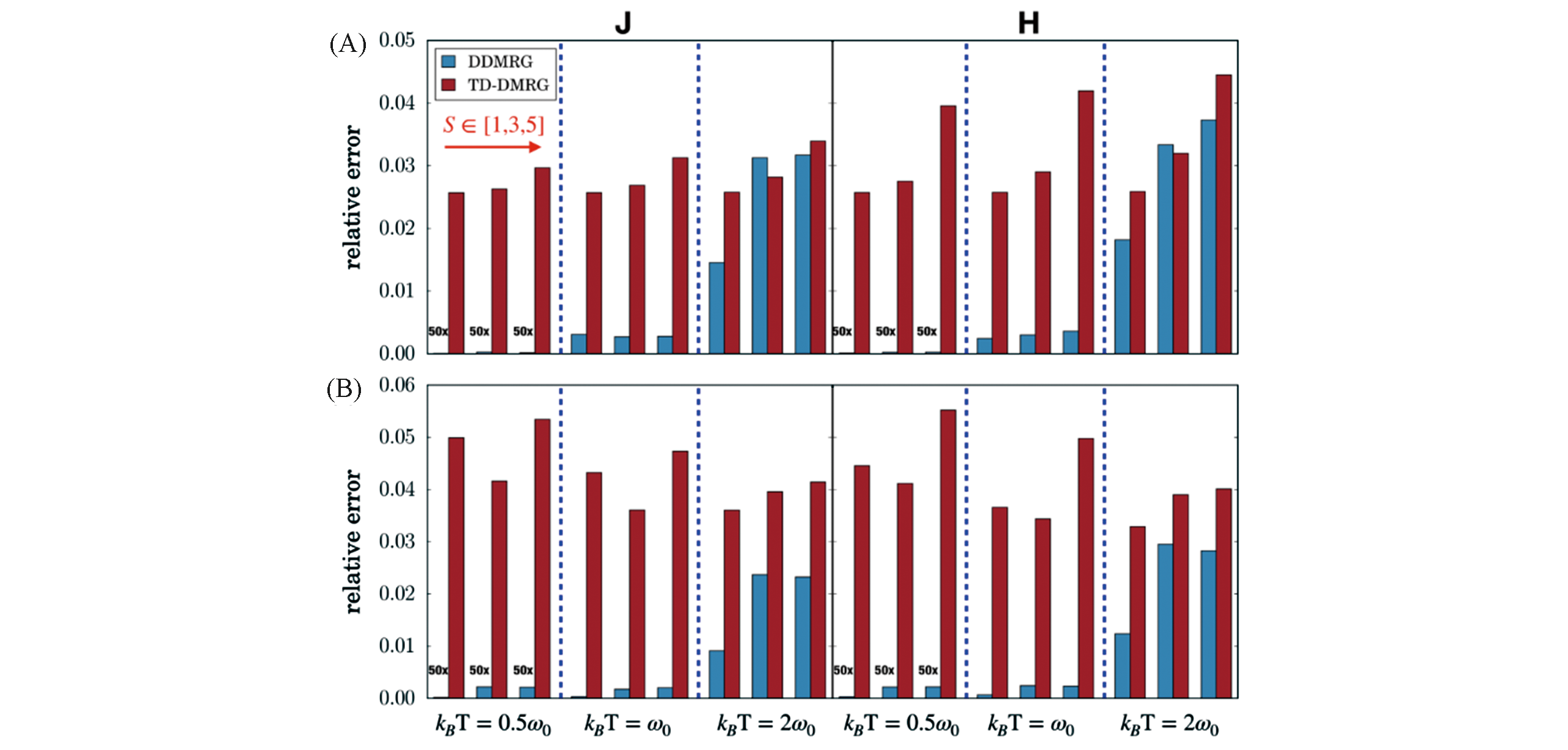
Fig.14 Graphical representation of molecular aggregates characterized by Holstein model

Fig.15 Relative error for J? and H?aggregates with different Huang?Rhys factor(S∈[1.0,3.0,5.0]) across different temperature(kBT∈[0.5ω0,ω0,2ω0])[22]Note the error of DDMRG at kBT=0.5ω0 is magnified by 50 times to make it clearly visible. (A) Absorption; (B) emission.Copyright 2020, American Chemical Society.

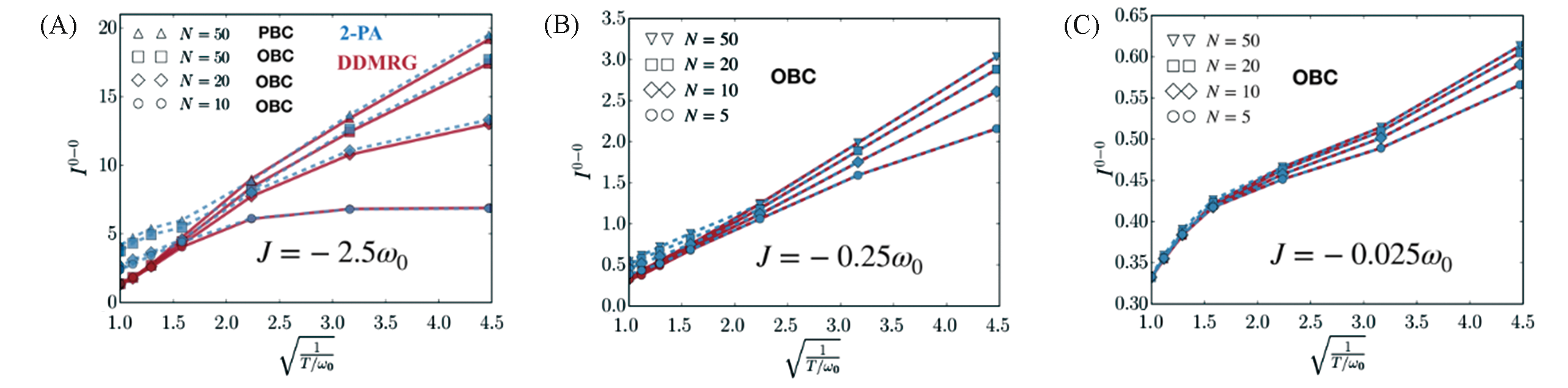
Fig.16 0?0 emission strength I0?0 as a function of T-1/2 for different excitonic coupling J0(A linear relation between them is predicted by strong excitonic coupling perturbation theory[59])[22](A) J0=-2.5ω0; (B) J0=-0.25ω0; (C) J0=-0.025ω0.Copyright 2020, American Chemical Society.

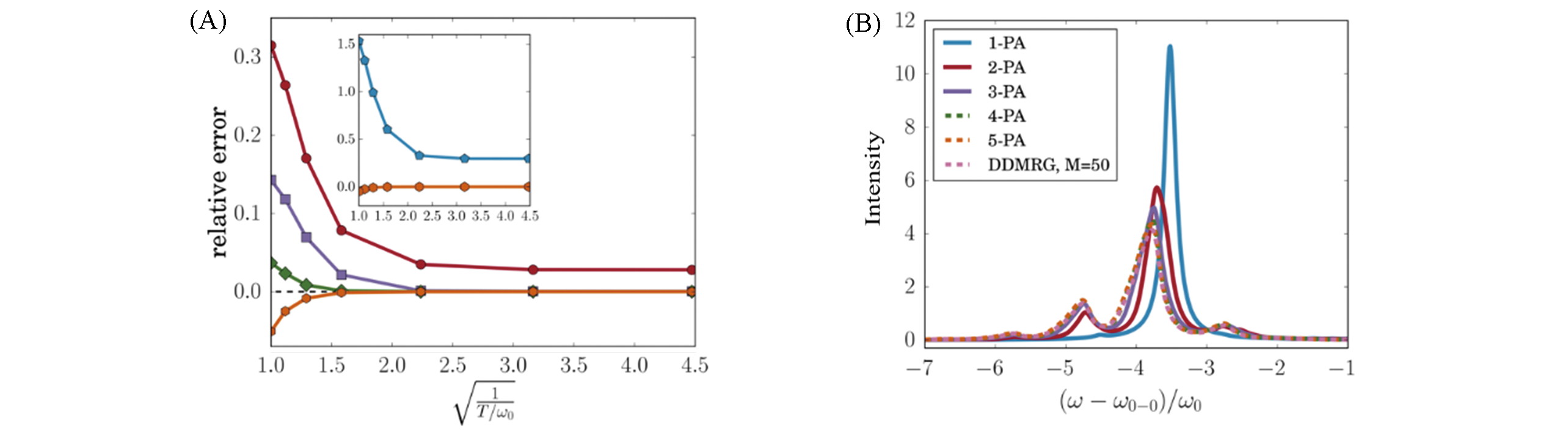
Fig.17 Comparison between DDMRG and n?particle approximation[22](A) Relative error of 0?0 emission strength of an open boundary 5?site system using n?particle approximation and DDMRG; (B) the emission spectrum at kBT=ω0 with broadening width η=0.1ω0, the pre?factor of the frequency index of the line strength is omitted.Copyright 2020, American Chemical Society.

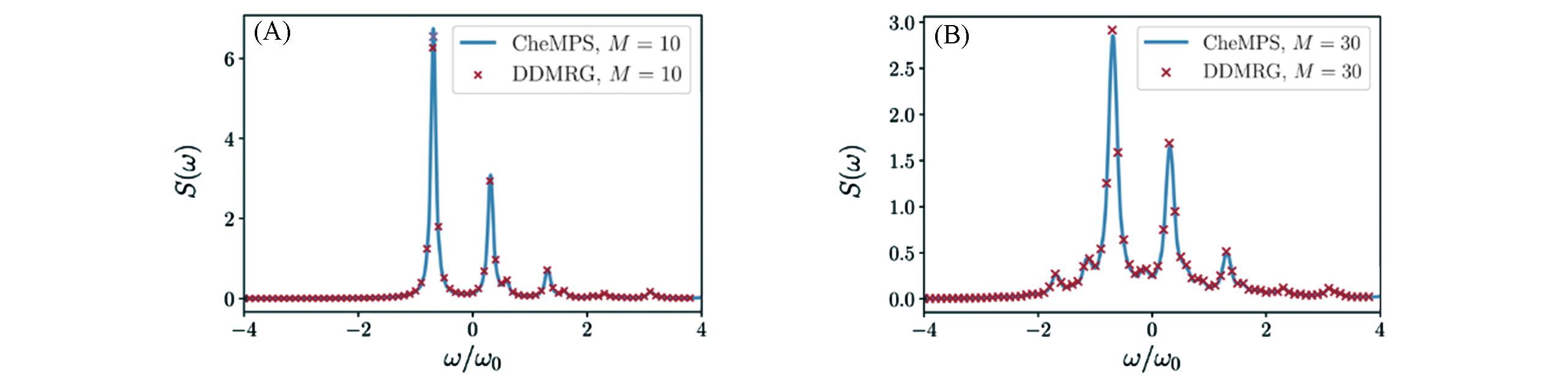
Fig.18 Linear absorption spectrum(omit the pre?factor of the frequency index) of dimer model using CheMPS and the comparison with DDMRG(A) At zero temperature T=0; (B)at finite temperature kBT=ω0/2.

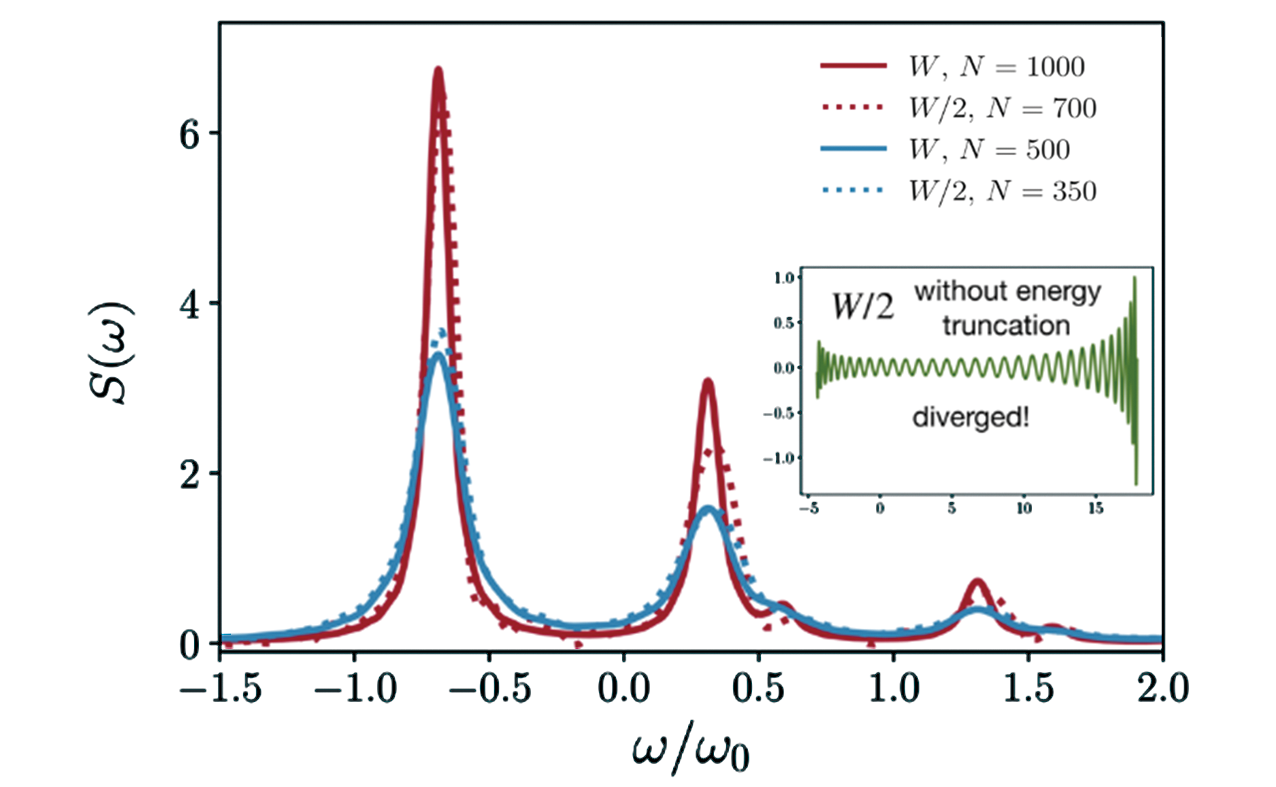
Fig.19 Linear absorption spectrum using different numbers of Chebyshev moments for expansion

Fig.20 Linear absorption spectrum calculated by using effective frequency window and the energy truncation scheme with the Krylov subspace dimension dk=10 and ns=1 sweep times

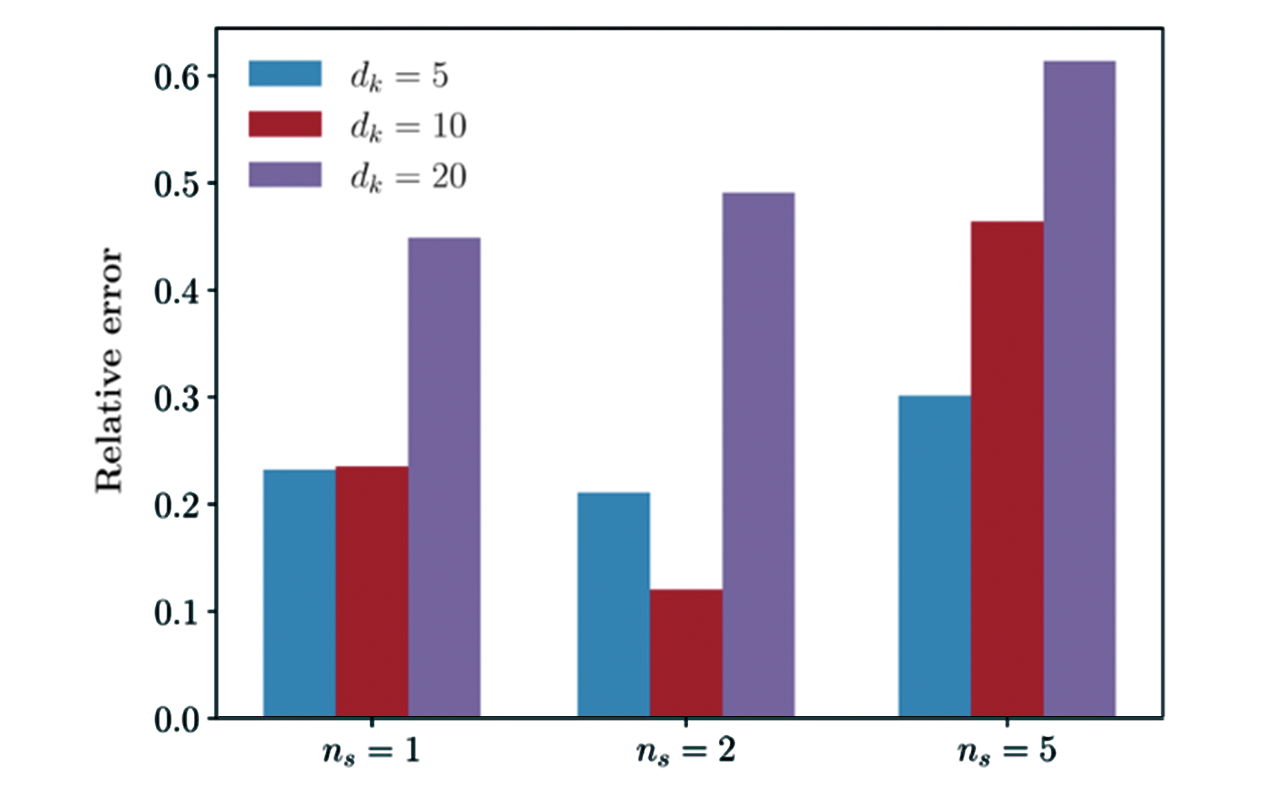
Fig.21 Relative error using effective band(W*=W/2) at N=700 with respect to the full many body band calculationat N=1000 for different combinations of Krylov subspace dimension dk and sweep times ns for energy truncation

参考文献 60

1	White S. R.， Phys. Rev. Lett.， 1992， 69（19）， 2863―2866
2	White S. R.， Phys. Rev. B： Condens. Matter Mater. Phys.， 1993， 48（14）， 10345―10356
3	Shuai Z.， Bredas J. L.， Pati S. K.， Ramasesha S.， Proc. SPIE， 1997， 3145， 293―302
4	Shuai Z.， Pati S. K.， Bredas J. L.， Ramasesha S.， Synth. Met.， 1997， 85（1―3）， 1011―1014
5	Ramasesha S.， Pati S. K.， Krishnamurthy H. R.， Shuai Z.， Brédas J. L.， Synth. Met.， 1997， 85， 1019―1022
6	Shuai Z.， Brédas J. L.， Saxena A.， Bishop A. R.， J. Chem. Phys.， 1998， 109， 2549―2555
7	Yaron D.， Moore E. E.， Shuai Z.， Brédas J. L.， J. Chem. Phys.， 1998， 108（17）， 7451―7458
8	Pati S. K.， Ramasesha S.， Shuai Z.， Brédas J. L.， Phys. Rev. B： Condens. Matter Mater. Phys.， 1999， 59（23）， 14827―14830
9	White S. R.， Martin R. L.， J. Chem. Phys.， 1999， 110（9）， 4127―4130
10	Chan G. K. L.， Head⁃Gordon M.， J. Chem. Phys.， 2002， 116（11）， 4462―4476
11	Vidal G.， Phys. Rev. Lett.， 2004， 93（4）， 40502
12	White S. R.， Feiguin A. E.， Phys. Rev. Lett.， 2004， 93（7）， 76401
13	Haegeman J.， Lubich C.， Oseledets I.， Vandereycken B.， Verstraete F.， Phys. Rev. B： Condens. Matter Mater. Phys.， 2016， 94（16）， 165116
14	Ronca E.， Li Z.， Jimenez⁃Hoyos C. A.， Chan G. K. L.， J. Chem. Theory Comput.， 2017， 13（11）， 5560―5571
15	Ren J.， Shuai Z.， Chan G. K. L.， J. Chem. Theory Comput.， 2018， 14（10）， 5027―5039
16	Li W.， Ren J.， Shuai Z.， J. Chem. Phys.， 2020， 152（2）， 24127
17	Hallberg K. A.， Phys. Rev. B： Condens. Matter Mater. Phys.， 1995， 52（14）， R9827
18	Dargel P. E.， Honecker A.， Peters R.， Noack R. M.， Pruschke T.， Phys. Rev. B： Condens. Matter Mater. Phys.， 2011， 83（16）， 161104
19	Dargel P. E.， Wöllert A.， Honecker A.， McCulloch I. P.， Schollwöck U.， Pruschke T.， Phys. Rev. B： Condens. Matter Mater. Phys.， 2012， 85（20）， 205119
20	Kühner T. D.， White S. R.， Phys. Rev. B： Condens. Matter Mater. Phys.， 1999， 60， 335―343
21	Jeckelmann E.， Phys. Rev. B： Condens. Matter Mater. Phys.， 2002， 66（4）， 045114
22	Jiang T.， Li W.， Ren J.， Shuai Z.， J. Phys. Chem. Lett.， 2020， 3761―3768
23	Holzner A.， Weichselbaum A.， McCulloch I. P.， Schollwöck U.， von Delft J.， Phys. Rev. B： Condens. Matter Mater. Phys.， 2011， 83（19）， 195115
24	Tiegel A. C.， Manmana S. R.， Pruschke T.， Honecker A.， Phys. Rev. B： Condens. Matter Mater. Phys.， 2014， 90（6）， 060406
25	Dorando J. J.， Hachmann J.， Chan G. K. L.， J. Chem. Phys.， 2009， 130（18）， 184111
26	Wouters S.， Nakatani N.， van Neck D.， Chan G. K. L.， Phys. Rev. B： Condens. Matter Mater. Phys.， 2013， 88（7）， 075122
27	Nakatani N.， Wouters S.， van Neck D.， Chan G. K. L.， J. Chem. Phys.， 2014， 140（2）， 24108
28	Yao Y.， Sun K. W.， Luo Z.， Ma H.， J. Phys. Chem. Lett.， 2018， 9（2）， 413―419
29	Greene S. M.， Batista V. S.， J. Chem. Theory Comput.， 2017， 13（9）， 4034―4042
30	Baiardi A.， Reiher M.， J. Chem. Theory Comput.， 2019， 15（6）， 3481―3498
31	Schröder F. A.， Turban D. H.， Musser A. J.， Hine N.D.， Chin A. W.， Nat. Commun.，2019， 10（1）， 1062
32	Xie X.， Liu Y.， Yao Y.， Schollwöck U.， Liu C.， Ma H.， J. Chem. Phys.， 2019， 151（22）， 224101
33	Gobert D.， Kollath C.， Schollwöck U.， Schütz G.， Phys. Rev. E， 2005， 71（3）， 36102
34	Barthel T.， Schollwöck U.， White S. R.， Phys. Rev. B： Condens. Matter Mater. Phys.， 2009， 79（24）， 245101
35	Kloss B.， Lev Y. B.， Reichman D.， Phys. Rev. B： Condens. Matter Mater. Phys.， 2018， 97， 024307
36	Ganahl M.， Thunström P.， Verstraete F.， Held K.， Evertz H. G.， Phys. Rev. B： Condens. Matter Mater. Phys.， 2014， 90（4）， 045144
37	Haegeman J.， Osborne T. J.， Verstraete F.， Phys. Rev. B： Condens. Matter Mater. Phys.， 2013， 88（7）， 075133
38	Schollwöck U.， Ann. Phys.， 2011， 326（1）， 96―192
39	Chan G. K. L.， Keselman A.， Nakatani N.， Li Z.， White S. R.， J. Chem. Phys.， 2016， 145（1）， 14102
40	Kubo R.， J. Phys. Soc. Japan， 1957， 12（6）， 570―586
41	Mahan G. D.， Many⁃Particle Physics， Springer Science & Business Media， Berlin， 2013
42	Gagliano E. R.， Balseiro C. A.， Phys. Rev. Lett.， 1987， 59（26）， 2999―3002
43	Zhang C.， Jeckelmann E.， White S. R.， Phys. Rev. B： Condens. Matter Mater. Phys.， 1999， 60（20）， 14092―14104
44	Yu W.， Haas S.， Phys. Rev. B： Condens. Matter Mater. Phys.， 2000， 63（2）， 024423
45	Okunishi K.， Akutsu Y.， Akutsu N.， Yamamoto T.， Phys. Rev. B： Condens. Matter Mater. Phys.， 2001， 64（10）， 104432
46	Garcia D. J.， Hallberg K.， Rozenberg M. J.， Phys. Rev. Lett.， 2004， 93（24）， 246403
47	Soos Z. G.， Ramasesha S.， J. Chem. Phys.， 1989， 90（2）， 1067―1076
48	Nocera A.， Alvarez G.， Phys. Rev. E， 2016， 94（5）， 053308
49	Silver R. N.， Röder H.， Int. J. Mod. Phys. C， 1994， 5（4）， 735―753
50	Wang L. W.， Phys. Rev. B： Condens. Matter Mater. Phys.， 1994， 49（15）， 10154―10158
51	Weiße A.， Eur. Phys. J. B⁃Condensed Matter Complex Syst.， 2004， 40（2）， 125―128
52	Weiße A.， Wellein G.， Alvermann A.， Fehske H.， Rev. Mod. Phys.， 2006， 78（1）， 275―306
53	Umezawa H.， Matsumoto H.， Tachiki M.， Thermo Field Dynamics and Condensed States， North Holland， Amsterdam， 1982
54	Verstraete F.， Garcia⁃Ripoll J. J.， Cirac J. I.， Phys. Rev. Lett.， 2004， 93（20）， 207204
55	Zwolak M.， Vidal G.， Phys. Rev. Lett.， 2004， 93（20）， 207205
56	Feiguin A. E.， White S. R.， Phys. Rev. B： Condens. Matter Mater. Phys.， 2005， 72（22）， 220401
57	Kokalj J.， Prelovšek P.， Phys. Rev. B： Condens. Matter Mater. Phys.， 2009， 80（20）， 205117
58	Renormalizer， https：//github.com/shuaigroup/Renormalizer
59	Spano F. C.， J. Chem. Phys.， 2004， 120（16）， 7643―7658
60	White S. R.， Phys. Rev. Lett.， 2009， 102（19）， 190601

[1]	李维唐, 任佳骏, 帅志刚. 含时密度矩阵重正化群的理论与应用[J]. 高等学校化学学报, 2021, 42(7): 2085.
[2]	孙润广, 张静, 郝长春, 陈莹莹, 杨谦. 脂筏微区超分子聚集体结构的稳定性[J]. 高等学校化学学报, 2011, 32(9): 2071.
[3]	李凯, 韩蛟, 张厚玉, ABRAMAVICIUS Darius, 张汉壮. 分子聚集体的光谱模拟[J]. 高等学校化学学报, 2011, 32(12): 2872.
[4]	袁建军, 李英顺, 李小琴, 张小红, 程时远, 江雷, 封麟先. 聚苯乙烯-b-聚氧乙烯-b-聚苯乙烯三嵌段共聚物的自组装[J]. 高等学校化学学报, 2003, 24(2): 371.
[5]	陈东明, 李晓原, 尤乃亭, 章应辉, 何天敬, 刘凡镇. 四-(对-磺基苯基)卟啉二酸(H₄²⁺TSPP)分子聚集体的共振喇曼光谱研究[J]. 高等学校化学学报, 1999, 20(7): 1097.
[6]	梁玉增, 李子臣, 李福绵. 两亲性含糖嵌段共聚物在水中分子聚集形态的转变[J]. 高等学校化学学报, 1999, 20(11): 1820.