长径比对椭球粒子液晶行为的影响

引用本文

徐明杰, 孙玉伟, 朱有亮, 付翠柳, 黄以能, 李占伟, 孙昭艳. 长径比对椭球粒子液晶行为的影响[J]. 高等学校化学学报, 2019,40(6): 1201-1206.
XU Mingjie, SUN Yuwei, ZHU Youliang, FU Cuiliu, HUANG Yineng, LI Zhanwei, SUN Zhaoyan. Effect of Aspect Ratio on Liquid Crystal Behavior of Ellipsoidal Particles^† [J]. Chemical Journal of Chinese Universities, 2019,40(6): 1201-1206.
Doi:10.7503/cjcu20190059 复制到剪切板

Permissions

长径比对椭球粒子液晶行为的影响

徐明杰^1,², 孙玉伟^2,³, 朱有亮^2,³, 付翠柳^2,³, 黄以能^1,⁴, 李占伟^2,³, 孙昭艳^1,^2,³

1. 伊犁师范大学物理科学与技术学院, 新疆凝聚态相变与微结构实验室, 伊宁 835000

2. 中国科学院长春应用化学研究所, 高分子物理与化学国家重点实验室, 长春 130022

3. 中国科学技术大学应用化学与工程学院, 合肥 230026

4. 南京大学物理学院, 固体微结构物理国家重点实验室, 南京 210093

联系人简介: 朱有亮, 男, 博士, 副研究员, 主要从事软物质体系的多尺度模拟研究. E-mail: youliangzhu@ciac.ac.cn;黄以能, 男, 博士, 教授. 主要从事相变与微结构动力学研究. E-mail: ynhuang@nju.edu.cn

收稿日期: 2019-01-21

基金资助: 国家重点研发计划项目(批准号: 2018YFB0703701)、国家自然科学基金(批准号: 21674116, 21790344, 21774129, 21833008)、中国科学院前沿科学重点研究项目(批准号: QYZDY-SSW-SLH027)和吉林省科技发展计划项目(批准号: 20190101021JH)资助.

摘要

利用Gay-Berne模型, 结合分子动力学模拟方法, 研究了粒子长径比对椭球粒子液晶行为的影响, 考察了粒子长径比对向列相和近晶相的影响. 结果表明, 长径比相对较小的粒子有利于向列相的形成, 而长径比相对较大的粒子更有利于近晶相的形成. 分析了近晶相和向列相形成的动力学过程.

关键词: 椭球粒子; 长径比; 向列相; 近晶相; Gay-Berne模型; 分子动力学

中图分类号:O641;O631 文献标志码:A

Effect of Aspect Ratio on Liquid Crystal Behavior of Ellipsoidal Particles^†

XU Mingjie^1,², SUN Yuwei^2,³, ZHU Youliang^2,³, FU Cuiliu^2,³, HUANG Yineng^1,⁴, LI Zhanwei^2,³, SUN Zhaoyan^1,^2,³

1. Xinjiang Laboratory of Phase Transitions and Microstructures in Condensed Matter Physics, College of Physical Science and Technology, Yili Normal University, Yining 835000, China

2. State Key Laboratory of Polymer Physics and Chemistry, Changchun Institute of Applied Chemistry, Chinese Academy of Sciences, Changchun 130022, China

3. University of Science and Technology of China, School of Applied Chemistry and Engineering, Hefei 230026, China

4. School of Physics, National Laboratory of Solid State Microstructures, Nanjing University, Nanjing 210093, China

Fund:† Supported by the National Key R&D Program of China(No.2018YFB0703701), the National Natural Science Foundation of China(Nos.21674116, 21790344, 21774129, 21833008) , the Key Research Program of Frontier Sciences, Chinese Academy of Sciences(No.QYZDY-SSW-SLH027) and the Jilin Provincial Science and Technology Development Program, China(No.20190101021JH).

Abstract

The Gay-Berne model and molecular dynamics simulation method was used to study the influences of aspect ratio on the liquid crystal behaviors of ellipsoidal particles, especially focusing on nematic and smectic phases. The results indicated that the ellipsoids with a relatively small aspect ratio favor the formation of nematic phases, while the ellipsoids with a relatively large aspect ratio prefer the formation of smectic phases. Furthermore, the formation processes of the nematic and smectic phases in detail were analyzed. The results provide theoretical guidance for designing different types of liquid crystals and understanding the formation mechanism of liquid crystal.

Keyword: Ellipsoidal particle; Aspect ratio; Nematic phase; Smectic phase; Gay-Berne model; Molecular dynamics

文章图片

液晶作为一种十分新奇的自然界中间态, 具有液体流动性和固体各向异性, 介于液体和晶体之间. 液晶由奥地利科学家Reinitzer^[1]在加热胆甾醇苯酸酯晶体时首先发现, 后经过德国物理学家Lehmann^[2]的进一步研究, 发现熔融得到的液体在形态上与普通液体相似, 但其光学性质与晶体相似, 具有各向异性的特点, 并且还观察到双折射现象. 液晶具有特殊的光电效应, 在干涉、散射、衍射和吸收等光学现象方面可以受电场调制, 所以液晶最主要的应用是作为显示材料, 如手机、电脑和电视的液晶显示板, 其优点在于功耗微小、显示信息量大及成本低廉等^[3]. 由于产生的条件不同, 液晶分为热致液晶和溶致液晶, 其中热致液晶又可分为向列相、近晶相和胆甾相, 通常, 显示材料用的是低分子热致液晶. 所以理解不同液晶形成的机理具有重要的实际应用价值和科学意义^[4].

计算机模拟研究液晶具有一定的优势, 目前, 一些常见的模型有简单格子模型^{[5, 6]}、硬椭球体模型、球体模型、 Gay-Berne(GB)模型^{[7, 8, 9]}、硬球柱模型以及球柱链模型^[10], 其中使用最广泛的是GB模型, 其除了体积排斥相互作用外还有吸引相互作用^[11]. 计算模拟研究发现, 棒状分子和盘状分子可以形成向列相, 并且在一些情况下, 通过调节分子大小和形状, 可以形成近晶相和柱状相, 所以分子形状及分子大小成为稳定液晶的关键因素^{[8, 12~15]}.

Deng等^[16]通过提出各向异性粒子的单粒子耗散动力学模型, 在更大尺度上研究了长径比对椭球粒子液晶行为的影响, 并分析了不同长径比体系的方向序参数变化. 但目前实验中具有不同长径比的粒子对液晶形成的规律尚不明确, 在实验中如何设计和使用具有不同长径比的粒子也不清楚. 因此, 本文采用GB粒子模型和分子动力学方法^{[17, 18, 19]} , 通过分析方向序参数和径向分布函数, 定量区分了不同的结构, 研究了粒子长径比对向列相和近晶相等相形貌的影响. 此外, 还分析了向列相和近晶相形成的动力学过程. 研究结果可为设计不同类型的液晶以及理解液晶的形成机理提供一定的理论指导.

1 计算模型与方法

使用单轴椭球模型描述了棒状分子, 所有模拟参数使用约化单位, 其中长度单位为σ _a, 能量单位为ε ₀, 质量单位为m₀, 时间单位为τ =(m₀/ε ₀)¹^/². GB势能U_GB(A_i, A_j, r_ij) 描述粒子的各向异性形状和相互作用的表达式为^{[20, 21, 22, 23, 24, 25, 26, 27, 28, 29, 30, 31]}

$U_{GB} (A_{i}, A_{j}, r_{ij}) = U_{r} (A_{i}, A_{j}, r_{ij}) η (A_{i}, A_{j}) χ (A_{i}, A_{j}, r_{ij}) (1)$

其中, U_GB(A_i, A_j, r_ij)依赖于2个椭球粒子之间最接近的距离h_ij和移位参数γ 来描述粒子间的相互作用, U_r(A_i, A_j, r_ij)可表示为

$U_{r} (A_{i}, A_{j}, r_{ij}) = 4 ε [{(\frac{σ}{h_{ij} + γσ})}^{12} - {(\frac{σ}{h_{ij} + γσ})}^{6}] (2)$

其中,

$\begin{array}{l} h_{ij} (A_{i}, A_{j}, r_{ij}) = r_{ij} - σ_{ij} (A_{i}, A_{j}, {\dot{r}}_{ij}) (3) \\ σ_{ij} (A_{i}, A_{j}, r_{ij}) = {[\frac{1}{2} {\dot{r}}^{Τ}_{ij} G_{ij}^{- 1} (A_{i}, A_{j}) {\dot{r}}_{ij}]}^{- 1 / 2} (4) \end{array}$

根据对角线形状矩阵S_i=diag(a_i, b_i, c_i)和S_j=diag(a_j, b_j, c_j), G_ij(A_i, A_j)可表示为

$\begin{array}{l} G_{ij} (A_{i}, A_{j}) = {A^{Τ}}_{i} S_{i}^{2} A_{i} + {A^{Τ}}_{j} S_{j}^{2} A_{j} (5) \\ η (A_{i}, A_{j}) = {[\frac{2 S_{i} S_{j}}{\det (G_{ij} (A_{i}, A_{j}))}]}^{ν / 2} (6) \end{array}$

基于椭球粒子的相对位置和取向, 式(1)中η $(A_{i}, A_{j})$ 和χ $(A_{i}, A_{j}, r_{ij})$ 共同控制各向异性相互作用强度:

$\begin{array}{l} S_{i} = (a_{i} b_{i} + c_{i} c_{i}) (a_{i} b_{i})^{1 / 2} (7) \\ χ (A_{i}, A_{j}, r_{ij}) = {[2 {\dot{r}}^{Τ}_{ij} B_{ij}^{- 1} (A_{i}, A_{j}) {\dot{r}}_{ij}]}^{μ} (8) \\ B_{ij} (A_{i}, A_{j}) = A_{i}^{Τ} E_{i} A_{i} + A_{j}^{Τ} E_{j} A_{j} (9) \end{array}$

其中, E_i=diag[(ε ₀/ε _ia)¹^/μ, (ε ₀/ε _ib)¹^/μ, (ε ₀/ε _ic)¹^/μ]和E_j=diag[(ε ₀/ε _ja)¹^/μ, (ε ₀/ε _jb)¹^/μ, (ε ₀/ε _jc)¹^/μ]为对角矩阵, μ 和ν 为经验值, 用来调整势能的大小.

图1描述了具有不同长径比的单轴椭球粒子头对头和肩并肩的相互作用势与粒子间距离的关系. 对于不同长径比的粒子, 选择相同的势井深度.

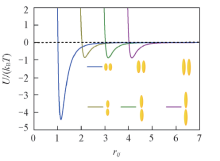	Figure Option View Download New Window
	Fig.1 Interaction potential(U) of uniaxial ellipsoids with different aspect ratio as a function of separation r_ij for side-by-side and end-to-end configurations

GB势的参数可以表示为GB(k, k^', μ , ν ), 其中k 表示长轴与短轴的比值, k^'表示椭球粒子肩并肩的势阱与头对头势阱的比值. 本文使用的参数为k^'=5, μ =1, ν =3. 这组参数是迄今使用最为广泛的参数组合, 且已有研究者给出了该体系的部分相图^[32]. 在正则系综(NVT)、长径比为3∶ 1的条件下, 采用与文献[22]一致的粒子数密度ρ =(N $σ_{a}^{3}$ )/V=0.3. 在其余的不同长径比体系中, 通过增加或减少粒子数以保证体系的体积分数与长径比为3∶ 1的体系相同. 此外, 保持粒子肩并肩相互作用势相同(约为4.62 k_BT)和头对头相互作用势相同(约为0.93 k_BT). 模拟采用具有周期性边界条件为30× 30× 30的立方盒子. 控温方式为Nosé -Hoover热浴, 积分步长为δ t=0.002τ . 每隔5× 10⁵τ 输出一次构象并进行表征, 每个体系总共模拟1× 10⁷τ , 并通过体系的扩散以及结构变化等信息判断以保证体系达到平衡. 所有模拟均采用GPU加速的大尺度分子动力学软件包GALAMOST^{[33, 34, 35]}.

2 结果与讨论

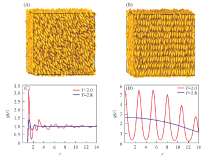采用分子动力学模拟方法验证文献[22]结果. 如图2(A)和(B)所示, 选取与文献[22]相同的数密度(ρ =0.3), 当温度(T)等于2.8时, 得到向列相; 当温度等于2.0时, 得到近晶相. 通过计算径向分布函数很容易区分有序相和无序相, 该函数给出距离原点r长度的范围内找到一个粒子的几率, 函数表达为 $g (r) = \frac{1}{4 π Nρ r^{2}} [\overset{n}{\sum_{i}} \overset{n}{\sum_{j \neq i}} δ (r - r_{ij})]$ (其中, N为体系总粒子数, ρ 为体系密度). 同时, 计算了平行于方向向量 $\vec{n}$ 的径向分布函数, 该函数对每层内粒子的排列方式非常敏感, 函数表达为 $g_{∥} r_{∥} = \frac{1}{π l_{t}^{2} Nρ} \{\overset{n}{\sum_{i}} \overset{n}{\sum_{j \neq i}} δ (r_{∥} - \vec{n} \cdot {\vec{r}}_{ij})\}$ (其中, r_􀰘为粒子i和j之间的距离 ${\vec{r}}_{ij}$ 在 $\vec{n}$ 方向的分量), 该函数给出了在以粒子i为原点, l_t为半径, 轴线平行于方向向量的圆柱内找到粒子j的几率. 通过对比径向分布函数[图2(C)]与平行径向分布函数[图2(D)]可见, 当温度等于2.0时, 有明显的层状结构; 当温度等于2.8时, 和液体类似, 没有层状结构. 由此, 可以定量区分向列相和近晶相, 与文献结果一致^[22]. 对于向列相和近晶相液晶结构, 由于其分子排列不同, 导致液晶的流动性不同, 可通过计算均方位移(MSD)对比二者的差异, 其函数定义为< r²(t)> = $\frac{1}{N}$ < $\overset{N}{\sum_{i}}$ [ ${\vec{r}}_{i}$ (t)- ${\vec{r}}_{i}$ (0)]²> , 其中, N为体系中粒子的个数. 不同温度下的MSD见图S1(见本文支持信息). 在长时间尺度下, 向列相液晶结构比近晶相液晶结构流动性好.

	Figure Option View Download New Window
	Fig.2 Snapshots at different temperatures of T=2.8(A) and T=2.0(B), radial distribution function g $(r)$ (C) and parallel radial distribution function g_‖ $(r_{‖})$ (D)

固定温度T=2.8不变, 在保证体积分数和相互作用势不变的情况下, 研究了粒子长径比对向列相的影响. 除了使用径向分布函数和平行径向分布函数来区分不同的相结构, 还计算了方向序参数< P₂> , 函数表达式为< P₂> = $\frac{3}{2}$ < ${(\dot{μ} \cdot \dot{e})}^{2}$ > - $\frac{1}{2}$ (其中, $\dot{μ}$ 为体系的方向向量, $\dot{e}$ 为粒子的方向向量), < P₂> 的数值用来表示粒子取向的有序度^{[36, 37, 38]}. 如图3(A)所示, 当长径比(c/a)< 2.395时, 体系为无序的液体; 当2.395< c/a< 3.8时, 形成向列相; 当c/a> 3.8时, 形成近晶相. 从图3(B)典型的径向分布函数可以清晰地区分结构, 当c/a=2.0时, 体系为无序液体; 当c/a> 3.0时, 出现长程有序结构. 从图3(C)中可以明显看出体系可形成很好的层状结构. 同时, 还统计了不同长径比体系在温度等于2.8时压力和能量随长径比的变化曲线, 见图S2(A)和(B)(见本文支持信息), 随着长径比的增加, 压力呈下降趋势, 能量呈上升趋势, 在无序相到向列相转变时变化较明显. 图4(A~D)给出了不同长径比的形貌图. 可见, 长径比较大的粒子更有利于近晶相的形成, 体系会由向列相转变为近晶相.

	Figure Option View Download New Window
	Fig.3 Characterization methods of order parameters < P₂> (A), radial distribution function g(r)(B) and parallel radial distribution function g_‖(r_‖)(C)

	Figure Option View Download New Window
	Fig.4 Snapshots for different aspect ratios at T=2.8 c/a: (A) 2∶ 1; (B) 3∶ 1; (C) 4∶ 1; (D) 5∶ 1.

保持T=2.0, 分析了粒子长径比对近晶相的影响, 通过模拟发现, 当c/a< 1.78时体系是一个无序相, c/a> 2.7时体系是近晶相[图5(A)]; 也可以分辨向列相和近晶相的差别, 当c/a> 2.7时, 有明显的层状结构形成[图5(B)和(C)]. 压力和能量随长径比的变化曲线(图S3, 见本文支持信息)显示, 压力随长径比的增加呈现下降趋势, 能量随着长径比的增加呈上升趋势. 图S4(见本文支持信息)给出了在相同温度T=2.0下不同长径比的形貌图, 并总结出如下规律: 长径比较大的粒子更有利于形成近晶相, 并且在一定程度上提高了有序度, 而长径比较小的粒子更趋向于形成向列相.

	Figure Option View Download New Window
	Fig.5 Different characterization methods of order parameters < P₂> (A), radial distribution function g $(r)$ (B) and parallel radial distribution function g_‖ $(r_{‖})$ (C)

由于常见的MC模拟很难给出向列相和近晶相形成的动力学过程, 因此, 采用MD的模拟方法进一步分析了向列相和近晶相的形成机理^[39]. 图6(A)~(D)给出了向列相在不同时刻的形貌图. 可见, 向列相的形成过程是首先形成局部有序的结构, 然后局部有序的范围不断变大, 最后形成向列相结构. 图6(E)~(H)为近晶相在不同时刻的形貌图. 可见, 该体系先形成局域有序的层状结构, 然后通过不断调整粒子的方向, 最终形成整体有序的层状结构.

	Figure Option View Download New Window
	Fig.6 Formation processes of the nematic phase in Fig.2(A)(A— D) and the smectic phase in Fig.2(B)(E— H) (A, E) 5.0× 10⁵τ ; (B, G) 7.0× 10⁵τ ; (C) 8.5× 10⁵τ ; (D) 1.0× 10⁶τ ; (F) 6.0× 10⁵τ ; (H) 9.0× 10⁵τ .

综上所述, 采用分子动力学模拟方法研究了长径比对椭球粒子液晶行为的影响, 由于温度对粒子的排列有很大影响, 长径比大的粒子间具有更强的相互作用, 会在更高温度下形成近晶相. 结果表明, 长径比较大的粒子更有利于近晶相的形成, 在一定程度上提高了近晶相有序度, 并且, 随着长径比的增加还会从向列相转变为近晶相. 长径比较小的粒子更有利于形成向列相, 随着长径比的降低, 向列相的有序度也在减小. 同时, 还分析了向列相和近晶相形成的动力学过程, 两者均是从局域有序逐渐调整为整体有序结构. 研究结果为实验设计不同类型的液晶提供了一定的理论指导, 也为理解不同液晶相的形成机理提供了重要的理论帮助.

支持信息见http://www.cjcu.jlu.edu.cn/CN/10.7503/cjcu20190059.

参考文献

文献列表

[1]	Reinitzer F. , Liq. Cryst. , 1989, 5(1), 7-18 [本文引用:1]
[2]	Lehmann O. , Ann. Phys. Berlin, 1900, 307(8), 649-705 [本文引用:1]
[3]	Pan Y. , Yang Y. L. , Chem. J. Chinese Universities, 1994, 15(12), 1868-1874 (潘懿, 杨玉良. 高等学校化学学报, 1994, 15(12), 1868-1874) [本文引用:1]
[4]	Zhang J. , Wang J. , Zhao L. , Yang W. , Bi M. , Wang Y. , Mu H. , Li Y. , Wang B. , Gao Y. , Li C. , Huang X. , Chem. Res. Chinese Universities, 2017, 33(5), 839-846 [本文引用:1]
[5]	Lebwohl P. A. , Lasher G. , Phys. Rev. A, 1972, 6(1), 426-429 [本文引用:1]
[6]	Fabbri U. Z. C. , Mol. Phys. , 1986, 58(4), 763-788 [本文引用:1]
[7]	Frenkel D. , Mol. Phys. , 1987, 60(1), 1-20 [本文引用:1]
[8]	Frenkel D. , Mulder B. M. , Mol. Phys. , 1985, 55(5), 1171-1192 [本文引用:2]
[9]	Gay J. G. , Berne B. J. , J. Chem. Phys. , 1981, 74(6), 3316-3319 [本文引用:1]
[10]	Zheng Y. X. , Yu Y. X. , Li Y. F. , Ind. Eng. Chem. Res. , 2011, 50(10), 6460-6469 [本文引用:1]
[11]	Yan L. T. , Xie X. M. , Prog. Polym. Sci. , 2013, 38(2), 369-405 [本文引用:1]
[12]	Eppenga R. , Frenkel D. , Mol. Phys. , 2006, 52(6), 1303-1334 [本文引用:1]
[13]	Demiguel E. , Rull L. F. , Chalam M. K. , Gubbins K. E. , Mol. Phys. , 1991, 74(2), 405-424 [本文引用:1]
[14]	Lebowitz J. L. , Perram J. W. , Mol. Phys. , 1983, 50(6), 1207-1214 [本文引用:1]
[15]	Eppenga R. , Frenkel D. , Mol. Phys. , 1984, 52(6), 1303-1334 [本文引用:1]
[16]	Deng M. , Pan W. , Karniadakis G. E. , J. Comput. Phys. , 2017, 336, 481-491 [本文引用:1]
[17]	Li Z. W. , Jia X. X. , Zhang J. , Sun Z. Y. , Lu Z. Y. , Acta Polym. Sin. , 2011, (9), 973-984 (李占伟, 贾晓溪, 张静, 孙昭艳, 吕中元. 高分子学报, 2011, (9), 973-984) [本文引用:1]
[18]	Huang Z. H. , Dong B. J. , Chen P. Y. , Yang Y. , Zhu G. L. , Yan L. T. , Acta Polym. Sin. , 2016, (8), 979-991 (黄子涵, 董伯骏, 陈鹏宇, 杨烨, 朱国龙, 燕立唐. 高分子学报, 2016, (8), 979-991) [本文引用:1]
[19]	Wu L. , Han Y. , Zhang Q. , Zhu L. , Zhang C. , Zhao R. , Chem. Res. Chinese Universities, 2018, 34(6), 939-944 [本文引用:1]
[20]	Li Z. W. , Zhu Y. L. , Lu Z. Y. , Sun Z. Y. , Soft Matter, 2018, 14(37), 7625-7633 [本文引用:1]
[21]	Gay J. G. , Berne B. J. , J. Chem. Phys. , 1981, 74(6), 3316-3319 [本文引用:1]
[22]	Zannoni C. , J. Mater. Chem. , 2001, 11(11), 2637-2646 [本文引用:5]
[23]	Care C. M. , Cleaver D. J. , Rep. Prog. Phys. , 2005, 68(11), 2665-2700 [本文引用:1]
[24]	Berardi R. , Costantini A. , Muccioli L. , Orland i S. , Zannoni C. , J. Chem. Phys. , 2007, 126(4), 044905 [本文引用:1]
[25]	Brown W. M. , Petersen M. K. , Plimpton S. J. , Grest G. S. , J. Chem. Phys. , 2009, 130(4), 044901 [本文引用:1]
[26]	Berardi R. , Fava C. , Zannoni C. , Chem. Phys. Lett. , 1995, 236(4/5), 462-468 [本文引用:1]
[27]	Berardi R. , Fava C. , Zannoni C. , Chem. Phys. Lett. , 1998, 297(1/2), 8-14 [本文引用:1]
[28]	Cleaver D. J. , Care C. M. , Allen M. P. , Neal M. P. , Phys. Rev. E: Stat. , 1996, 54(1), 559-567 [本文引用:1]
[29]	Li Z. W. , Liu Y. H. , Liu Y. T. , Lu Z. Y. , Sci. China Chem. , 2011, 54(9), 1474-1483 [本文引用:1]
[30]	Madsen L. A. , Samulski E. T. , Liq. Cryst. , 2005, 32(11/12), 1419-1425 [本文引用:1]
[31]	Yang S. , Zhu Y. , Qian H. , Lu Z. , Chem. Res. Chinese Universities, 2017, 33(2), 261-267 [本文引用:1]
[32]	De Miguel E. , Rull L. F. , Chalam M. K. , Gubbins K. E. , Mol. Phys. , 1991, 74(2), 405-424 [本文引用:1]
[33]	Zhu Y. L. , Liu H. , Li Z. W. , Qian H. J. , Milano G. , Lu Z. Y. , J. Comput. Chem. , 2013, 34(25), 2197-2211 [本文引用:1]
[34]	Zhu Y. L. , Pan D. , Li Z. W. , Liu H. , Qian H. J. , Zhao Y. , Lu Z. Y. , Sun Z. Y. , Mol. Phys. , 2018, 116(7/8), 1065-1077 [本文引用:1]
[35]	Li Z. W. , Sun Z. Y. , Lu Z. Y. , Sci. China Chem. , 2017, 60(3), 109-133 [本文引用:1]
[36]	Berardi R. , Emerson A. P. J. , Zannoni C. , J. Chem. Soc. Faraday Trans. , 1993, 89(22), 4069-4078 [本文引用:1]
[37]	Li Z. W. , Chen L. J. , Zhao Y. , Lu Z. Y. , J. Phys. Chem. B, 2008, 112(44), 13842-13848 [本文引用:1]
[38]	Li Z. W. , Sun Z. Y. , Lu Z. Y. , J. Phys. Chem. B, 2010, 114(7), 2353-2358 [本文引用:1]
[39]	Wang T. , Hong K. , Zhang H. D. , Yang Y. L. , Chem. J. Chinese Universities, 2006, 27(1), 187-191 (王涛, 洪珂, 张红东, 杨玉良. 高等学校化学学报, 2006, 27(1), 187-191) [本文引用:1]

1989

0.0

... 液晶由奥地利科学家Reinitzer^[1]在加热胆甾醇苯酸酯晶体时首先发现, 后经过德国物理学家Lehmann^[2]的进一步研究, 发现熔融得到的液体在形态上与普通液体相似, 但其光学性质与晶体相似, 具有各向异性的特点, 并且还观察到双折射现象 ...

1900

0.0

1994

0.0

... 液晶具有特殊的光电效应, 在干涉、散射、衍射和吸收等光学现象方面可以受电场调制, 所以液晶最主要的应用是作为显示材料, 如手机、电脑和电视的液晶显示板, 其优点在于功耗微小、显示信息量大及成本低廉等^[3] ...

2017

0.0

... 所以理解不同液晶形成的机理具有重要的实际应用价值和科学意义^[4] ...

1972

0.0

... 计算机模拟研究液晶具有一定的优势, 目前, 一些常见的模型有简单格子模型^[5,6]、硬椭球体模型、球体模型、 Gay-Berne(GB)模型^[7,8,9]、硬球柱模型以及球柱链模型^[10], 其中使用最广泛的是GB模型, 其除了体积排斥相互作用外还有吸引相互作用^[11] ...

1986

0.0

1987

0.0

1985

0.0

... 计算模拟研究发现, 棒状分子和盘状分子可以形成向列相, 并且在一些情况下, 通过调节分子大小和形状, 可以形成近晶相和柱状相, 所以分子形状及分子大小成为稳定液晶的关键因素^{[8, 12~15]} ...

1981

0.0

2011

0.0

2013

0.0

2006

0.0

1991

0.0

1983

0.0

1984

0.0

2017

0.0

... Deng等^[16]通过提出各向异性粒子的单粒子耗散动力学模型, 在更大尺度上研究了长径比对椭球粒子液晶行为的影响, 并分析了不同长径比体系的方向序参数变化 ...

2011

0.0

. W. , Jia X. X. , Zhang J. , Sun Z. Y. , Lu Z. Y. , Acta Polym. Sin. , 2011, (9), 973-984

(李占伟, 贾晓溪, 张静, 孙昭艳, 吕中元. 高分子学报, 2011, (9), 973-984)

Amphiphilic block copolymers in selective solutions can self-assemble into various morphologies, such as spherical, rodlike and disklike micelles, bilayer membranes, vesicles and nanotubes. These aggregated nano-structures are of great potential in drug delivery, microelectronics and advanced material applications. Therefore, it is very important to study the phase behaviors of block copolymers and understand the formation mechanism of complex aggregated nano-structures. Due to the complexity of these aggregated nano-structures, computer simulations can be used as a powerful tool to study the phase behaviors of block copolymers. In this review, we mainly cover recent developments in the field of mesoscopic computer simulations of structure design for block copolymers. Specifically, dissipative particle dynamics simulations, self-consistent field theory dynamic density functional theory and Monte Carlo simulations will be the main themes in this review.

[Li Zhanwei; Sun Zhaoyan] Chinese Acad Sci, Changchun Inst Appl Chem, State Key Lab Polymer Phys & Chem, Changchun 130022, Peoples R China.;[Jia Xiaoxi; Zhang Jing; Lu Zhongyuan] Jilin Univ, State Key Lab Theoret & Computat Chem, Inst Theoret Chem, Changchun 130023, Peoples R China.

嵌段共聚物在本体或在选择性溶剂中可以通过微相分离或自组装形成各种各样的纳米结构,如层状相、球状、棒状及碟状胶束、双层膜、囊泡、纳米管等.这些纳米结构在药物输送、微电子学、先进材料等领域具有令人瞩目的应用前景.因此,研究嵌段共聚物形成纳米有序结构的过程以及理解复杂纳米结构的形成机理具有非常重要的意义.由于嵌段共聚物纳米聚集结构的复杂性,计算机模拟目前已成为研究嵌段共聚物微相分离和自组装的重要手段之一.主要综述了介观模拟方法在嵌段共聚物纳米结构设计方面的一些重要进展,其中将对耗散粒子动力学、自洽场理论方法、动态密度泛函理论、蒙特卡罗模拟方法进行重点阐述.

... 因此, 本文采用GB粒子模型和分子动力学方法^[17,18,19] , 通过分析方向序参数和径向分布函数, 定量区分了不同的结构, 研究了粒子长径比对向列相和近晶相等相形貌的影响 ...

2016

0.0

2018

0.0

2018

0.0

... GB势能U_GB(A_i,A_j,r_ij) 描述粒子的各向异性形状和相互作用的表达式为^{[20,21,22,23,24,25,26,27,28,29,30,31]} ...

1981

0.0

... GB势能U_GB(A_i,A_j,r_ij) 描述粒子的各向异性形状和相互作用的表达式为^{[20,21,22,23,24,25,26,27,28,29,30,31]} ...

2001

0.0

... GB势能U_GB(A_i,A_j,r_ij) 描述粒子的各向异性形状和相互作用的表达式为^{[20,21,22,23,24,25,26,27,28,29,30,31]} ...

... 1的条件下, 采用与文献[22]一致的粒子数密度#cod#x003c1 ...

... 2 结果与讨论采用分子动力学模拟方法验证文献[22]结果 ...

... 如图2(A)和(B)所示, 选取与文献[22]相同的数密度(#cod#x003c1 ...

... 由此, 可以定量区分向列相和近晶相, 与文献结果一致^[22] ...

2005

0.0

... GB势能U_GB(A_i,A_j,r_ij) 描述粒子的各向异性形状和相互作用的表达式为^{[20,21,22,23,24,25,26,27,28,29,30,31]} ...

2007

0.0

... GB势能U_GB(A_i,A_j,r_ij) 描述粒子的各向异性形状和相互作用的表达式为^{[20,21,22,23,24,25,26,27,28,29,30,31]} ...

2009

0.0

... GB势能U_GB(A_i,A_j,r_ij) 描述粒子的各向异性形状和相互作用的表达式为^{[20,21,22,23,24,25,26,27,28,29,30,31]} ...

1995

0.0

... GB势能U_GB(A_i,A_j,r_ij) 描述粒子的各向异性形状和相互作用的表达式为^{[20,21,22,23,24,25,26,27,28,29,30,31]} ...

1998

0.0

... GB势能U_GB(A_i,A_j,r_ij) 描述粒子的各向异性形状和相互作用的表达式为^{[20,21,22,23,24,25,26,27,28,29,30,31]} ...

1996

0.0

... GB势能U_GB(A_i,A_j,r_ij) 描述粒子的各向异性形状和相互作用的表达式为^{[20,21,22,23,24,25,26,27,28,29,30,31]} ...

2011

0.0

... GB势能U_GB(A_i,A_j,r_ij) 描述粒子的各向异性形状和相互作用的表达式为^{[20,21,22,23,24,25,26,27,28,29,30,31]} ...

2005

0.0

... GB势能U_GB(A_i,A_j,r_ij) 描述粒子的各向异性形状和相互作用的表达式为^{[20,21,22,23,24,25,26,27,28,29,30,31]} ...

2017

0.0

... GB势能U_GB(A_i,A_j,r_ij) 描述粒子的各向异性形状和相互作用的表达式为^{[20,21,22,23,24,25,26,27,28,29,30,31]} ...

1991

0.0

... 这组参数是迄今使用最为广泛的参数组合, 且已有研究者给出了该体系的部分相图^[32] ...

2013

0.0

... 所有模拟均采用GPU加速的大尺度分子动力学软件包GALAMOST^[33,34,35] ...

2018

0.0

... 所有模拟均采用GPU加速的大尺度分子动力学软件包GALAMOST^[33,34,35] ...

2017

0.0

... 所有模拟均采用GPU加速的大尺度分子动力学软件包GALAMOST^[33,34,35] ...

1993

0.0

... 的数值用来表示粒子取向的有序度^[36,37,38] ...

2008

0.0

... 的数值用来表示粒子取向的有序度^[36,37,38] ...

2010

0.0

... 的数值用来表示粒子取向的有序度^[36,37,38] ...

2006

0.0

... 由于常见的MC模拟很难给出向列相和近晶相形成的动力学过程, 因此, 采用MD的模拟方法进一步分析了向列相和近晶相的形成机理^[39] ...