以时温等效方法研究尼龙1010应力松弛行为及使用寿命预测

引用本文

蔡利海, 郭宝华, 张诚, 徐军, 黄忠耀. 以时温等效方法研究尼龙1010应力松弛行为及使用寿命预测[J]. 高等学校化学学报, 2019,40(4): 832-840.
CAI Lihai, GUO Baohua, ZHANG Cheng, XU Jun, HUANG Zhongyao. Long-term Stress Relaxation Prediction for Nylon 1010 Using Time-temperature Superposition Method^† [J]. Chemical Journal of Chinese Universities, 2019,40(4): 832-840.
Doi:10.7503/cjcu20180685 复制到剪切板

Permissions

以时温等效方法研究尼龙1010应力松弛行为及使用寿命预测

蔡利海, 郭宝华, 张诚, 徐军, 黄忠耀

清华大学化学工程系, 先进材料教育部重点实验室, 北京 100084

联系人简介: 郭宝华, 男, 教授, 主要从事高分子材料方面的研究. E-mail: bhguo@mail.tsinghua.edu.cn

收稿日期: 2018-10-10

基金资助: 国家自然科学基金(批准号:51473085, 51673110)、国家自然科学基金联合基金(批准号:U1862205)和清华大学苏州创新引领专项基金(批准号:2016SZ0315)资助.

摘要

以尼龙材料的应力松弛行为作为研究对象, 考察初始应变为1.0%, 2.8%和5.1%的尼龙1010样品在温度区间293353 K的松弛曲线, 采用时间-温度等效叠加方法得到了松弛模量主曲线, 计算出叠加过程中的表观活化能、松弛过程中的活化体积和应力辅助功. 结果表明, 整个松弛过程中的表观活化能和应力辅助功表现出相同的变化趋势, 体现出松弛过程中克服运动单元位垒的过程. 当293323 K区间的松弛曲线叠加时, 随着初始应变的增加, 表观活化能和应力辅助功均逐渐降低, 有助于聚合物内部的运动单元越过能垒发生松弛, 与松弛过程中的应力辅助热活化理论相一致; 当333353 K区间的松弛曲线叠加时, 不同初始应变样品的表观活化能均为260 kJ/mol, 应力辅助功均为60 MPa·nm³, 说明松弛过程中克服运动单元的能垒与应力作用无关. 根据松弛主曲线, 计算出了尼龙1010在1.0%, 2.8%和5.1% 3种形变下, 长时间范围内应力衰减与时间的关系, 为预测实际使用过程中的应力松弛行为提供了依据.

关键词: 尼龙1010; 应力松弛; 时间-温度等效叠加; 活化能; 活化体积; 应力辅助功

中图分类号:O631 文献标志码:A

Long-term Stress Relaxation Prediction for Nylon 1010 Using Time-temperature Superposition Method^†

CAI Lihai, GUO Baohua^*, ZHANG Cheng, XU Jun, HUANG Zhongyao

Department of Chemical Engineering, Key Lab of Advanced Materials of Ministry of Education, Tsinghua University, Beijing 100084, China

Fund:† Supported by the National Natural Science Foundation of China(Nos.51473085, 51673110), the Joint Funds of the National Natural Science Foundation of China(No.U1862205)and the Tsinghua University-Suzhou Innovation Leading Program, China(No.2016SZ0315).

Abstract

Stress relaxation behavior of plastic has great influence on its service life and safety. The master curves were generated by horizontal and vertical shifts of the short term curves of stress relaxation for Nylon 1010 at temperatures ranging from 293 K to 353 K using proposed time-temperature superposition equivalence method. The apparent activation energy was calculated from the Arrhenius plots of shift factor, and the values of activation volume and stress-assisted work were calculated from the master curves. The time-temperature superposition principle was found to be available for the stress relaxation curves. During the superposition interval of the experimental temperature from 293 K to 323 K, the apparent activation energy and stress-assisted work show a tendency to decrease gradually, which is helpful for the relaxation of the moving units in the polymer over the energy barrier. During the superposition interval of the experimental temperature from 333 K to 353 K, the apparent activation energy of different initial strain samples is about the same value of 260 kJ/mol and the stress-aided work is basically unchanged at the value of 60 MPa·nm³, which indicates that the energy barrier of the moving unit is independent of the stress effect. According to the mater curves of Nylon 1010, the relationship between stress decay and relaxation time in a long time range can be obtained under the strain of 1.0%, 2.8% and 5.1%, which provides a reference for predicting stress relaxation behavior in practical use.

Keyword: Nylon 1010; Stress relaxation; Time-temperature superposition; Apparent activation energy; Activation volume; Stress-aided work

文章图片

工程塑料以其质量轻、耐腐蚀及成型加工性能好等优点作为金属材料的轻量化替代品, 广泛用于工业各个领域, 其中作为结构件和紧固件, 在长期使用中因应力衰减导致性能不能满足要求是一种典型的失效模式, 研究材料的应力衰减特性, 掌握长时间范围内的应力衰减规律是需要解决的重要理论和应用问题^[1]. 目前, 对于长时间范围内应力衰减行为的研究, 主要通过对实验测试的应力松弛曲线进行数学归纳得到松弛过程的动力学方程^{[2, 3, 4, 5, 6, 7, 8]}, 或者建立模型对应力松弛曲线进行模拟^{[9, 16]}, 从而预测出应力衰减失效时间. 研究发现, 对于一些结晶性聚合物在长时间的应力松弛过程中存在着不同的松弛机理^{[2, 17, 18]}, 即单一的动力学方程或数学模型不能反映实际的时间-应力特性; 在实验室进行单个样品的应力松弛实验由于时间较短难以推导出长时间实际使用中的应力衰减规律. 根据聚合物在一定条件下温度和外力作用时间对其力学性能影响具有等效关系的特点^[19], 通过系列环境温度下实验得到的应力松弛曲线, 采用时间-温度等效叠加方法, 推导出常温下长时间的应力衰减行为来预测应力失效时间、确定使用寿命是可行的方法.

尼龙1010是重要的工程塑料^{[20, 35]}, 从20世纪70年代开始广泛应用于机械、化工及航空航天等多个领域, 我国对该材料的合成路线^[20]、结构性能表征^{[21, 28]}、加工特性分析^{[29, 30]}和使用性能评估^{[32, 34]}等方面进行了系统研究, 但长期应力下的应力衰减行为研究还有待深入.

时间-温度等效叠加方法通过测试聚合物不同温度下的模量-时间松弛曲线, 以一个确定的温度为参考, 将不同温度下的松弛模量曲线沿对数时间坐标平行和垂直移动至叠合, 得到聚合物在参考温度下较长时间的应力衰减行为^{[19, 36]}. 时间-温度等效叠加方法最早应用于无定型聚合物松弛行为的时间-温度转换研究^[1]. 研究发现, 半晶型聚合物在满足一定条件后也可以使用该方法^{[37, 40]}. 这是由于以下3方面原因: (1) 应力松弛的初始应变在应力-应变曲线的线性区域; (2) 松弛样品在实验之前需要进行预处理以减小松弛过程中聚集态结构的变化; (3) 松弛过程中聚合物不应发生化学结构的改变. 目前, 时间-温度等效叠加方法已经广泛应用于半晶型聚合物的应力松弛研究^{[41, 45]}.

本文针对尼龙材料单次应力松弛实验难以测试出长时间范围内应力衰减的问题, 探讨以时温等效叠加方法进行尼龙1010应力松弛行为研究的可行性以及长时间范围内的应力衰减规律, 预测材料工程应用中的使用寿命; 分析时温等效叠加计算出的表观活化能随松弛时间增加和应力衰减时的变化关系, 研究松弛过程中分子运动单元需克服能垒的变化, 进一步探索半晶型聚合物长时间范围内的应力松弛机理.

1 实验部分

1.1 试剂与仪器

尼龙1010应力松弛初始样品为挤出棒材, 直径 30 mm, 原材料为上海市赛璐璐厂产品. 树脂的相对黏度1.61, 加工后应力松弛测试段直径 13 mm, 长 95 mm. 应力松弛采用河北承德金建仪器公司的万能材料试验机测试, 初始应变拉伸速率为5 mm/min; TMA-60型热机械分析(TMA)仪, 日本Shimadzu公司, 采用膨胀模式, 测试温度283393 K, 升温速率5 K/min, 样品直径2 mm, 长度8 mm; Q2000型示差扫描量热仪(DSC), 美国TA公司, 测试温度233493 K, 升温速度10 K/min; Rigaku R-Axis Spider X射线分析仪, 装配成像系统, 射线源为金属钼, 扫描区域为200 μ m× 200 μ m, 测试电压50 kV, 测试电流80 mA, 曝光时间600 s, 样品尺寸30 mm× 12 mm× 2.5 mm.

1.2 应力松弛曲线的时间-温度叠加方法

应力松弛曲线参考文献[34]中的数据. 为了增加不同温度下曲线的重合区域, 参考文献[34]实验方法在323 K时进行了初始应变为1.0%, 2.8%和5.1%的应力松弛实验, 得到尼龙1010在293353 K间隔为10 K的应力松弛曲线. 在此基础上, 按照式(1)将应力-时间曲线转换为模量-时间坐标(图1), 然后根据时间-温度叠加原理^[19], 以293 K为参考温度, 将不同温度下的曲线沿对数时间坐标轴移动, 多条曲线叠加后得到样品在参考温度下长时间范围的模量-时间主曲线.

$E (t) = σ (t) / ε (t) (1)$

式中: σ 为松弛应力; ε 为应变; E为松弛模量.

曲线叠加时分为水平移动和垂直移动两步^[19]. 水平移动参考式(2)(4)进行:

$\begin{array}{l} E (t, T_{1}) = [ρ (T_{1}) T_{1} / ρ (T_{2}) T_{2}] E (t / α_{T}, T_{2}) (2) \\ \lg E (t, T_{1}) = \lg [ρ (T_{1}) T_{1} / ρ (T_{2}) T_{2}] + \lg E (t / α_{T}, T_{2}) (3) \\ \lg α_{T} = \lg t - \lg t_{1} (4) \end{array}$

式中: ρ 为样品密度; t为松弛时间; T₁和t₁分别为参考温度和平移后的时间; T₂为实验温度; α _T为平移因子, 是保持曲线形状不变条件下的时间标尺位移量^[19].

曲线叠加时的垂直移动参考下式进行:

$\begin{array}{l} β_{T} = \frac{ρ (T_{1}) T_{1}}{ρ (T_{2}) T_{2}} = \frac{V (T_{2}) T_{1}}{V (T_{1}) T_{2}} = \frac{[V (T_{1}) + V (T_{1}) \int_{T_{1}}^{T_{2}} α_{V} d T] T_{1}}{V (T_{1}) T_{2}} = \\ (1 + \int_{T_{1}}^{T_{2}} α_{V} d T) \frac{T_{1}}{T_{2}} \approx (1 + 3 \int_{T_{1}}^{T_{2}} α_{l} d T) \frac{T_{1}}{T_{2}} (5) \\ α_{V} = \frac{1}{V_{0}} {(\frac{\partial V}{\partial T})}_{p}, α_{l} = \frac{1}{L_{0}} {(\frac{\partial L}{\partial T})}_{p} (6) \end{array}$

式中: ρ (T₁)T₁/[ρ (T₂)T₂]可用β _T表示, 为垂直修正因子, 是曲线在垂直方向的移动量, β _T值与密度和温度2个参数相关. 式(6)中V₀为松弛段样品初始体积; α _V为体积膨胀系数, 表示随着环境温度的变化, 样品体积变化与初始体积之比; α _l为线膨胀系数, 表示随着环境温度的变化时松弛段样品长度变化与初始长度之比; L₀为松弛段样品初始长度. 对于膨胀系数较小的各向同性材料, 体积膨胀系数可按线膨胀系数的3倍计算^[46], 实验中通过测试线膨胀系数来计算β _T.

	Figure Option View Download New Window
	Fig.1 Relaxation modulus of relaxation samples under different initial strains (A) 1.0% strain; (B) 2.8% strain; (C) 5.1% strain. 293 K; 303 K; 313 K; 323 K; 333 K; 343 K; 353 K.

2 结果与讨论

2.1 样品松弛前后的结构表征

对于半晶型聚合物, 在采用时温等效原理进行松弛曲线的叠加时, 应尽量减小松弛前后样品取向程度和结晶度等聚集态结构的变化^[37], 因此样品在松弛实验之前进行了退火处理, 并且实验时将初始应变控制在应力-应变曲线的线性区域^[34].

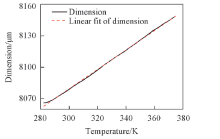
图2为尼龙1010样品线膨胀性测试曲线. 可以看出, 在293 K时, 样品长度L_{293 K}约为8.07 mm, 随着温度的升高, 曲线斜率基本不变, 在玻璃化转变温度附近未出现明显的转折, 线膨胀系数可以看作1个常数. 通过对曲线的线性拟合, 得到曲线的斜率b为0.93, 根据式(7)计算出线膨胀系数为1.16× 10^-4 K^-1. 将该值代入式(5)中, 能够计算出不同温度下的β _T值.

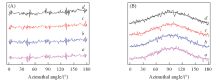
$α_{l} = \frac{(L_{1} - L_{2})}{L_{293 K} (T_{1} - T_{2})} \approx \frac{b}{L_{293 K}} (7)$

图3为初始应变为5.1%时, 不同温度下尼龙1010样品应力松弛实验后, 沿拉伸方向制备的厚度为2.5 mm的薄片的二维X射线衍射图. 可以看到, 在应力松弛实验前后, 不同初始应变样品的衍射图均出现了3个衍射环, 由内到外分别对应于尼龙1010的(002), (100)和(110/010) 3个晶面方位角的衍射^[23], 样品呈现典型的尼龙α 晶型^[31]. 图4(A)为图3中(002)晶面衍射的Azimuthal图. 可以看出, 尼龙1010样品在松弛实验前后均未产生衍射峰, 样品的(002)取向为0. 图4(B)为图3中(100)晶面衍射的Azimuthal图. 曲线经高斯拟合后计算^[47]得到的取向度列于表1. 可以看到, 松弛实验前后样品的(100)取向无明显改变(51.2%).

	Figure Option View Download New Window
	Fig.2 Fitting the dimension in linear expansion test of Nylon 1010

	Figure Option View Download New Window
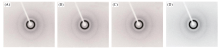	Fig.3 X-Ray diffraction patterns of Nylon 1010 samples (A) Initial; (B) 5.1% strain at 293 K; (C) 5.1% strain at 313 K; (D) 5.1% strain at 353 K.

	Figure Option View Download New Window
	Fig.4 Azimuthal X-ray diffraction intensity curves of Nylon 1010 samples (A) (002) reflection; (B) (100) reflection. a. Initial; b. 5.1% strain at 293 K; c. 5.1% strain at 313 K; d. 5.1% strain at 353 K.

Table 1 Crystallinity(X_c) and orientation degree(Π ) of Nylon 1010 samples

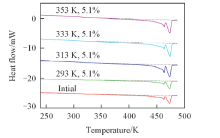
针对样品松弛前后可能产生的热物理参数变化, 对松弛前后的吸放热性能进行了DSC测试, 得到应力松弛前后样品在环境温度变化时的吸放热值, 根据式(8)对比松弛前后结晶度的差别. 其中Δ H为熔融焓, Δ $H_{m}^{0}$ 为外推条件下完全结晶时的熔融焓^[25], X_c(%)为依据DSC熔融焓计算出的结晶度.

$X_{c} = \frac{Δ H}{Δ H^{0}_{m}} \times 100 % (8)$

图5为初始应变为5.1%时, 尼龙1010在不同温度下进行应力松弛实验前后的DSC曲线. 由式(8)相应的熔融焓计算的结晶度见表1. 可以看出, 松弛实验前后各样品的DSC曲线形状和Δ H值均未出现明显的差别, 说明松弛实验前后样品没有明显的结晶度(38.4%)变化. 此外, 在温度为 318 K 附近的尼龙1010玻璃化转变温度区^[34], 图5中曲线没有出现明显的吸热峰, 与图2中线膨胀曲线没有突然转折的现象相对应, 说明样品在松弛实验前的热处理提高了聚集态结构的稳定性.

	Figure Option View Download New Window
	Fig.5 DSC curves of Nylon 1010 samples

2.2 应力松弛曲线的时间-温度叠加

以293 K为参考温度, 通过时间-温度叠加方法得到不同初始应变下的松弛模量主曲线, 结果如图6所示. 可以看出, 对于不同温度下的松弛曲线进行叠加时, 3条主曲线在大部分的叠加区均重合较好, 只是在松弛的初始阶段, 相邻2条曲线会出现偏差. 这种现象与Hejlova等^[8]和Gupta等^[48]的实验结果相同. 这是由于在松弛的初始阶段, 应变刚刚达到预定值, 样品处于由强制拉伸到突然静止的状态, 分子链在失去了强制的拉伸应力时, 产生很大的反作用力, 松弛速率快速增加至最大值^[34]. 由于这一阶段的松弛并不完全是由分子自发的热运动造成的, 所以在曲线叠加时与相邻的温度曲线不重合. 参考Hejlova等^[8]的工作, 曲线叠加时不考虑初始阶段不重合的部分, 同时为方便对松弛主曲线进行计算, 本文绘制的松弛模量主曲线也只考虑不同温度下松弛曲线的重合部分.

	Figure Option View Download New Window
	Fig.6 Master curves of relaxation modulus for the samples in the strain of 1.0%(A), 2.8%(B) and 5.1%(C)

2.3 平移因子和表观活化能

图7为平移因子(α _T)与温度的关系. 可以看出, 在323333 K温度范围内, 不同初始应变曲线存在着转折区, 该温度区域正是尼龙1010的玻璃化转变区. 说明了在玻璃化转变温度前后应力松弛的机理并不相同, 依据阿累尼乌斯方程^[49], 相应计算出的松弛过程中与温度相关的表观活化能也会有所差别.

	Figure Option View Download New Window
	Fig.7 Temperature dependence of logarithm of shift factor for the samples (A) lnα _T and T; (B) lnα _T and T^-1.

将图7(A)中的坐标转换为lnα _T与绝对温度的倒数关系, 如图7(B)所示. 参考下式:

$Δ H_{a} = R \frac{d (\ln α_{T})}{d (T^{- 1})} (9)$

式中: Δ H_α为松弛过程中的表观活化能, 表示松弛过程中的温度依赖性^[49]; R 为气体常数. 将293323和333353 K的平移因子分别拟合计算出活化能, 结果见表2.

Table 2 Apparent activation energies(Δ H_a) in Arrhenius plots of Fig.6

从表2可以看出, 在实验温度范围为293323 K时, 随着样品松弛时初始形变的增加, 表观活化能逐渐降低. 原因是随着初始应变的增加, 样品受到的应力更大, 强迫聚合物内部的运动单元越过能垒发生松弛, 即松弛克服的能垒降低, 表观活化能呈现出逐渐降低的趋势, 与应力辅助的热活化理论相对应^[34]. 当温度大于333 K时, 3个样品松弛过程中的表观活化能均为260 kJ/mol, 与样品初始应变无关. 原因是在此时较高的环境温度下, 1.0%应变的应力辅助作用已使链段可以自由运动(尼龙1010的T_g为343 K), 因此在更高的应力作用下促进松弛的效果与1.0%应变时应力促进松弛的效果基本相同, 活化单元都表现为链段运动.

2.4 松弛主曲线的应力辅助功分析

研究^[34]发现尼龙1010在应力松弛过程中会先后呈现2种机理: (1) 松弛的初始阶段, 应力有助于聚合物运动单元能垒的降低, 松弛行为满足应力辅助热活化理论; (2) 松弛过程中应力辅助功近似不变的阶段. 由于在单个温度下松弛实验的时间相对较短, 单次实验下松弛曲线不能很好地区分2种机理产生的条件. 将图6的松弛模量叠加主曲线去除相邻实验温度曲线中初始阶段不重合的部分, 得到3种初始应变下的松弛模量叠加主曲线, 其活化体积和应力辅助功也应该与293 K时间实验下的松弛曲线具有相似的变化规律, 因此可以利用叠加主曲线来分析随着等效松弛时间增加或应力衰减下的松弛机理.

根据叠加主曲线计算出对应的时间坐标、松弛应力与应力辅助功的关系如图8所示. 其中应力辅助功为活化体积与松弛过程中真应力的乘积, 活化体积^[50]的计算如下:

$\begin{array}{l} σ_{0} = E_{0} ε (10) \\ σ^{*} = σ - σ_{\infty} (11) \\ V_{a} = kT {[\frac{\partial \ln (- d σ / d t)}{\partial σ^{*}}]}_{T} (12) \end{array}$

式中: σ ₀和E₀为初始应力和初始模量; σ ^*为松弛过程中的真应力; σ _∞为残余应力, 对于初始应变为1.0%, 2.8%和5.1%的残余应力分别为1.8, 5.2和10.0 MPa^[34]; V_a为活化体积; σ ^*V_a为应力辅助功, 指聚合物运动单元从当前位置跃迁到下一位置时应力所做的功^[50]; k为波尔兹曼常数.

	Figure Option View Download New Window
	Fig.8 Curves of σ ^V_a vs. lgt(A) and σ ^(B) calculated from the master curves of Fig.6

由图8(A)可以看出, 在松弛初始阶段, 相同时间段下随着初始应变的增加应力辅助功逐渐降低, 参考图6, 该时段对应的实验温度处于323 K 以下松弛曲线叠加段, 与表观活化能随初始应变的增加逐渐降低的趋势一致, 在此阶段初始应力越大, 样品松弛越容易, 即应力有助于聚合物内部的运动单元越过能垒发生松弛, 导致松弛活化能和松弛能垒的降低, 因此从表观活化能的角度解释了松弛过程中的应力辅助热活化理论. 随着松弛时间的增加, 对应于玻璃化转变温度以上的松弛曲线叠加段, 计算出的表观活化能近似恒定, 说明此阶段松弛过程中克服运动单元的能垒与应力作用无关, 相应图8(A)中3种初始应变的应力辅助功均为60 MPa· nm³. 图8(B)为不同初始应变下松弛应力的衰减与应力辅助功的关系. 可以看出, 不同的初始应变产生初始应力值不同, 但随着应力的衰减, 应力辅助功均逐渐减小至定值后基本保持不变; 对于不同初始应变下应力辅助功均逐渐减小, 不重合的曲线部分对应于表观活化能下降的阶段, 应力辅助功保持不变的部分对应于表观活化能近似恒定的阶段. 综合以上2种情况, 整个松弛过程中的表观活化能和应力辅助功均表现出先下降后为定值的相同变化趋势, 分别对应于应力辅助热活化松弛机理和活化单元协同运动松弛机理.

2.5 尼龙1010在工程使用中松弛失效时间预测

进行应力松弛研究最重要的工程应用是掌握零部件在实际使用中的应力下降情况, 预测松弛失效时间. 根据松弛模量主曲线, 以年度为横坐标, 分别以剩余应力和剩余应力与初始应力比值为纵坐标, 计算出了尼龙1010在 1.0%, 2.8%和5.1% 3种形变下实际应力的下降情况, 结果如图9所示. 由图9(D)可以看出, 随着初始形变的增加, 松弛过程中应力衰减的速度相应增加, 以应力衰减到初始应力的70%为例, 可以计算出初始应变为5.1%, 2.8%和1.0%样品的应力衰减时间分别为2 h, 15 d和16 a. 参考图9(A)(C)可以计算出, 其初始应力分别为56, 31和11 MPa, 应力下降为初始应力70%时残余的应力分别为39, 23和8 MPa.

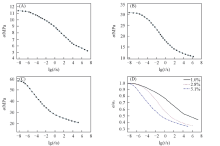	Figure Option View Download New Window
	Fig.9 Master curves of relaxation samples under the initial strains of 1.0%(A), 2.8%(B), 5.1%(C) and the comparison of different strains(D)

针对尼龙1010应力松弛曲线特性, 由于该材料玻璃化转变温度较低, 因此常温下保持其固定形变时, 在应力辅助作用下因形变产生的应力容易使运动单元活化, 表观活化能降低, 进入应力辅助的热活化松弛阶段, 此时的松弛速率会快速增加, 从而应力松弛现象更为明显.

3 结论

尼龙1010样品应力松弛前后结晶度和取向度均未出现明显的差别, 按照时间-温度叠加方法得到的松弛模量主曲线重合良好, 整个松弛过程中的表观活化能和应力辅助功表现出相同的变化趋势. 在松弛初始阶段, 相同时间范围内随着初始应变的增加表观活化能逐渐降低, 即应力有助于聚合物内部的运动单元越过能垒发生松弛, 符合应力辅助热活化理论; 在随后的松弛阶段, 不同初始应变样品的表观活化能保持定值, 说明此时松弛过程中克服运动单元的能垒与应力作用无关, 与长时间松弛后应力辅助功保持恒定的现象一致. 根据松弛模量主曲线, 计算出了尼龙1010在1.0%, 2.8%和5.1% 3种形变下, 长时间范围内应力衰减与时间的关系, 为预测尼龙1010材料实际使用过程中的应力松弛行为提供了依据.

参考文献

文献列表

[1]	Tobolsky A. V. , J. Appl. Phys. , 1956, 27(7), 673—685 [本文引用:2]
[2]	Dotsenko V. I. , Phys. Status Solidi B, 1979, 93(1), 11—43 [本文引用:2]
[3]	Kubat J. , Nilsson L. A. , Rigdahl M. , Mater. Sci. Eng. ,1982, 53(2), 199—208 [本文引用:1]
[4]	Kubat J. , Nilsson L. A. , Mater. Sci. Eng. ,1982, 52(3), 223—228 [本文引用:1]
[5]	Kubat J. , Rigdahl M. , Selden R. , J. Appl. Polym. Sci. ,1976, 20(10), 2799—2809 [本文引用:1]
[6]	Lu Y. , Yang W. , Zhang K. , Yang M. B. , Polym. Test. ,2010, 29(7), 866—871 [本文引用:1]
[7]	Mohomane S. , Djokovic V. , Thomas S. , Luyt A. S. , Polym. Test. ,2011, 30(5), 585—593 [本文引用:1]
[8]	Hejlova A. , Blahovec J. , Polym. Eng. Sci. ,2015, 55(3), 624—633 [本文引用:3]
[9]	Razavi-Nouri M. , Iran. J. Chem. Eng. , 2012, 9(1), 60—69 [本文引用:1]
[10]	Bagley R. L. , Torvik P. , J. Rheol. ,1983, 27(3), 201—210 [本文引用:1]
[11]	Dobreva A. , Gutzow I. , Schmelzer J. , J. Non-Cryst. Solids, 1997, 209(3), 257—263 [本文引用:1]
[12]	Fancey K. S. , J. Mater. Sci. , 2005, 40(18), 4827—4831 [本文引用:1]
[13]	Ghosh A. , Das S. , Banerjee D. , Indian J. Fibre Text. Res. ,2013, 38(4), 375—379 [本文引用:1]
[14]	Koeller R. C. , J. Appl. Mech. , 1984, 51(2), 299—307 [本文引用:1]
[15]	Chen Y. , Chen H. S. , Kang Y. G. , Chem. J. Chinese Universities, 2006, 27(11), 2160—2163 (陈艳, 陈宏善, 康永刚. 高等学校化学学报, 2006, 27(11), 2160—2163) [本文引用:1]
[16]	Chen H. S. , Li M. M. , Kang Y. G. , Zhang S. L. , Chem. J. Chinese Universities, 2008, 29(6), 1271—1275 (陈宏善, 李明明, 康永刚, 张素玲. 高等学校化学学报, 2008, 29(6), 1271—1275) [本文引用:1]
[17]	Kubat J. , Nilsson L. A. , Rigdahl M. , Mater. Sci. Eng. ,1983, 61(3), 267—274 [本文引用:1]
[18]	Kubat J. , Selden R. , Rigdahl M. , J. Appl. Polym. Sci. ,1978, 22(6), 1715—1723 [本文引用:1]
[19]	Shaw M. T. , Macknight W. J. , Introduction to Polymer Viscoelasticity(3rd Ed. ), Translated by Li Y. N. , East China University of Science and Technology Press, Shanghai, 2012, 117—121 (李怡宁[译]李怡宁[译]. 聚合物黏弹性引论(第三版), 上海: 华东理工大学出版社, 2012, 82—98) [本文引用:5]
[20]	Zeng H. M. , Chen H. M. , Chem. J. Chinese Universities, 1986, 7(12), 1140—1145 (曾汉民, 陈海宁. 高等学校化学学报, 1986, 7(12), 1140—1145) [本文引用:2]
[21]	Lv Y. F. , Yang X. Z. , Zhu S. N. , Li X. K. , Acta Chim. Sin. , 1983, (6), 525—533 (吕亚非, 杨小震, 朱善农, 李相魁. 化学学报, 1983, (6), 525—533) [本文引用:1]
[22]	Yang X. Z. , Hu S. R. , Lv Y. F. , Zhu S. N. , Li X. K. , Polym. Commun. , 1985, (3), 202—206 (杨小震, 胡世如, 吕亚非, 朱善农, 李相魁. 高分子通讯, 1985, (3), 202—206) [本文引用:1]
[23]	Mo Z. S. , Zhang H. F. , Meng Q. B. , Xue X. F. , Zhang L. H. , Acta Polym. Sin. , 1990, (6), 655—660 (莫志深, 张宏放, 孟庆波, 薛小芙, 张利华. 高分子学报, 1990, (6), 655—660) [本文引用:1]
[24]	Fu S. R. , Zhang G. , Tan Q. , Yang Y. , J. Therm. Anal. ,1993, 40(2), 689—695 [本文引用:1]
[25]	Feng J. H. , Mo Z. S. , Chen D. L. , Chinese J. Polym. Sci. ,1990, 8(1), 61—68 [本文引用:1]
[26]	Zhu C. S. , Li X. D. , Pu S. T. , Chem. J. Chinese Universities, 1991, 12(12), 1677—1680 (朱诚身, 李修道, 李华光, 蒲帅天. 高等学校化学学报, 1991, 12s(12), 1677—1680) [本文引用:1]
[27]	Zhu C. S. , Mo Z. S. , Mou Z. C. , Chem. J. Chinese Universities, 1992, 13(6), 864—866 (朱诚身, 莫志深, 牟忠诚. 高等学校化学学报, 1992, 13(6), 864—866) [本文引用:1]
[28]	Mo Z. S. , Meng Q. B. , Feng J. H. , Zhang H. F. , Chen D. L. , Polym. Int. ,1993, 32(1), 53—60 [本文引用:1]
[29]	Zeng H. M. , Chen H. N. , Chem. J. Chinese Universities, 1986, 7(9), 851—856 (曾汉民, 陈海宁. 高等学校化学学报, 1986, 7(9), 851—856) [本文引用:1]
[30]	Zhu C. S. , Chen Y. , Yang G. P. , Wang Y. W. , Wang J. W. , Mo Z. S. , Chem. J. Chinese Universities, 1996, 17(5), 805—807 (朱诚身, 陈玉, 杨桂萍, 王友文, 王经武, 莫志深. 高等学校化学学报, 1996, 17(5), 805—807) [本文引用:1]
[31]	Wang J. K. , Zhao G. S. , Zhou Y. C. , Chem. J. Chinese Universities, 2011, 32(5), 1225—1230 (王继库, 赵国升, 周云春. 高等学校化学学报, 2011, 32(5), 1225—1230) [本文引用:1]
[32]	Lu H. B. , Zhang X. Y. , Zhang H. , J. Appl. Phys. ,2006, 100(054104), 1—7 [本文引用:1]
[33]	Lu H. B. , Zhang X. Y. , J. Macromol. Sci. Part B, 2006, 45(5), 933—944 [本文引用:1]
[34]	Cai L. H. , Zhang C. , Guo B. H. , Xu J. , Huang Z. Y. , Acta Polym. Sin. , 2016, (3), 382—390 (蔡利海, 张诚, 郭宝华, 徐军, 黄忠耀. 高分子学报, 2016, (3), 382—390) [本文引用:9]
[35]	Cai L. H. , Qi Z. G. , Xu J. , Guo B. H. , Huang Z. Y. , Chinese Chem. Lett. ,2017, 28(5), 949—954 [本文引用:1]
[36]	Ferry J. D. , J. Am. Chem. Soc. , 1950, 72(8), 3746—3752 [本文引用:1]
[37]	Nagamatsu K. , Kolloid Z. , 1960, 172(2), 141—162 [本文引用:2]
[38]	Nagamatsu K. , Yoshitomi T. , J. Colloid Sci. ,1959, 14(4), 377—384 [本文引用:1]
[39]	Yoshitomi T. , Nagamatsu K. , Kosiyama K. , J. Appl. Polym. Sci. ,1958, 27(115), 335—347 [本文引用:1]
[40]	Nagamatsu K. , Yoshitomi T. , Takemoto T. , J. Colloid Sci. ,1958, 13(3), 257—265 [本文引用:1]
[41]	Williams M. L. , Bender M. F. , J. Appl. Phys. ,1965, 36(10), 3044—3049 [本文引用:1]
[42]	Murayama T. , Dumbleton J. H. , Williams M. L. , J. Macromol. Sci. , Part B, 1967, 1(1), 1—14 [本文引用:1]
[43]	Tajvidi M. , Falk R. H. , Hermanson J. C. , J. Appl. Polym. Sci. ,2005, 97(5), 1995—2004 [本文引用:1]
[44]	Nakano T. , Mech. Time-Depend Mater. , 2013, 17(3), 439—447 [本文引用:1]
[45]	Zhang J. , Jiang H. , Jiang C. , Kang G. , Lu F. , Polym. Test. ,2015, 44(7), 8—14 [本文引用:1]
[46]	Van Krevelen D. W. , Nijenhuis K. T. , Properties of Polymers(4th Ed. ), Science Press, Beijing, 2010, 89—101 [本文引用:1]
[47]	Mo Z. S. , Zhang H. F. , Zhang J. D. , Structure of Crystalline Polymers by X-Ray Diffraction(2nd Ed. ), Science Press, Beijing, 2003, 234 (莫志深, 张宏放, 张吉东. 晶态聚合物结构和X射线衍射(第2版), 北京: 科学出版社, 2003, 234) [本文引用:1]
[48]	Gupta V. , Rao D. R. , J. Appl. Polym. Sci. ,1992, 45(2), 253—263 [本文引用:1]
[49]	William M. , Land el R. , Ferry J. , J. Am. Chem. Soc. ,1955, 77(14), 3701—3707 [本文引用:2]
[50]	Brostow W. , Corneliussen R. D. , Failure of Plastics, Hanser Press, New York, 1986, 60—83 [本文引用:2]

1956

0.0

... 工程塑料以其质量轻、耐腐蚀及成型加工性能好等优点作为金属材料的轻量化替代品, 广泛用于工业各个领域, 其中作为结构件和紧固件, 在长期使用中因应力衰减导致性能不能满足要求是一种典型的失效模式, 研究材料的应力衰减特性, 掌握长时间范围内的应力衰减规律是需要解决的重要理论和应用问题^[1] ...

... 时间-温度等效叠加方法最早应用于无定型聚合物松弛行为的时间-温度转换研究^[1] ...

1979

0.0

... 目前, 对于长时间范围内应力衰减行为的研究, 主要通过对实验测试的应力松弛曲线进行数学归纳得到松弛过程的动力学方程^{[2,3,4,5,6,7,8]}, 或者建立模型对应力松弛曲线进行模拟^[9,16], 从而预测出应力衰减失效时间 ...

... 研究发现, 对于一些结晶性聚合物在长时间的应力松弛过程中存在着不同的松弛机理^[2,17,18], 即单一的动力学方程或数学模型不能反映实际的时间-应力特性 ...

1982

0.0

1982

0.0

1976

0.0

2010

0.0

2011

0.0

2015

0.0

... 这种现象与Hejlova等^[8]和Gupta等^[48]的实验结果相同 ...

... 参考Hejlova等^[8]的工作, 曲线叠加时不考虑初始阶段不重合的部分, 同时为方便对松弛主曲线进行计算, 本文绘制的松弛模量主曲线也只考虑不同温度下松弛曲线的重合部分 ...

2012

0.0

1983

0.0

1997

0.0

2005

0.0

2013

0.0

1984

0.0

2006

0.0

2008

0.0

1983

0.0

1978

0.0

2012

0.0

... 根据聚合物在一定条件下温度和外力作用时间对其力学性能影响具有等效关系的特点^[19], 通过系列环境温度下实验得到的应力松弛曲线, 采用时间-温度等效叠加方法, 推导出常温下长时间的应力衰减行为来预测应力失效时间、确定使用寿命是可行的方法 ...

... 时间-温度等效叠加方法通过测试聚合物不同温度下的模量-时间松弛曲线, 以一个确定的温度为参考, 将不同温度下的松弛模量曲线沿对数时间坐标平行和垂直移动至叠合, 得到聚合物在参考温度下较长时间的应力衰减行为^[19,36] ...

... 在此基础上, 按照式(1)将应力-时间曲线转换为模量-时间坐标(图1), 然后根据时间-温度叠加原理^[19], 以293 K为参考温度, 将不同温度下的曲线沿对数时间坐标轴移动, 多条曲线叠加后得到样品在参考温度下长时间范围的模量-时间主曲线 ...

... 曲线叠加时分为水平移动和垂直移动两步^[19] ...

... _T为平移因子, 是保持曲线形状不变条件下的时间标尺位移量^[19] ...

1986

0.0

... 尼龙1010是重要的工程塑料^[20,35], 从20世纪70年代开始广泛应用于机械、化工及航空航天等多个领域, 我国对该材料的合成路线^[20]、结构性能表征^[21,28]、加工特性分析^[29,30]和使用性能评估^[32,34]等方面进行了系统研究, 但长期应力下的应力衰减行为研究还有待深入 ...

1983

0.0

Y. F

. , Yang

X. Z

. , Zhu

S. N

. , Li

X. K

. , Acta Chim. Sin. , 1983, (6), 525—533

(吕亚非, 杨小震, 朱善农, 李相魁. 化学学报, 1983, (6), 525—533)

The changes of infrared spectra and densities for Nylon 1010 under various conditions of heat treatment were studied. The polarized infrared spectra of the sample oriented by stretching were also recorded. From the factor group analysis and the normal vibrational modes comparison, a great deal of symmetry species, polarization benaviors and selective rules are obtained in terms of their symmetry properties, then the infrared bands are assigned. Some new bands which are discodvered by means of separating overlapping spectral bands with computer have been discussed.

1985

0.0

1990

0.0

Z. S

. , Zhang

H. F

. , Meng

Q. B

. , Xue

X. F

. , Zhang

L. H

. , Acta Polym. Sin. , 1990, (6), 655—660

(莫志深, 张宏放, 孟庆波, 薛小芙, 张利华. 高分子学报, 1990, (6), 655—660)

From X-ray diffraction patterns of uniaxially oriented fibers, the crystal structure of Nylon-1010 was determined. The Nylon-1010 crystallizes in the triclinic system, with lattice dimensions: a = 4.9A, b = 5Ak, c = 27.8A, α = 49°, β = 77°, γ= 63.5°, the unit cell contains one monomeric unit and the space group is PI. The degree of crystallinity of polymer was determined as about 60%, using Ruland's method.SAXS has been used to investigate the crystalline lamellar thickness, long periods, transition zones,the specific inner surface andan electron density difference between the crystal-line and amorphous regions for Nylon-1010,the analysis of data was based upon the one-dim-ensional electrondensity correlation function (EDCF).

Laboratory of Polymer Physics; Changchun Institute of Applied Chemistry; Academia Sinica; Changchun

用WAXD方法测定了Nylon-1010为三斜晶系结晶结构;α=4.9A,b=5.4A,c=27.8(?),α=49°,β=77°,γ=63.5°,每个聚合物单胞含有一个重复单元,空间群为PA。模压试样用Ruland方法分析结晶度为60％。以上。电子密度相关函数法分析了SAXS现象,求得了Nylon-1010结晶片层厚度、过渡层厚度、长周期、比内表面及电子密度差。

... 可以看到, 在应力松弛实验前后, 不同初始应变样品的衍射图均出现了3个衍射环, 由内到外分别对应于尼龙1010的(002), (100)和(110/010) 3个晶面方位角的衍射^[23], 样品呈现典型的尼龙#cod#x003b1 ...

1993

0.0

1990

0.0

... Hm0为外推条件下完全结晶时的熔融焓^[25], X_c(%)为依据DSC熔融焓计算出的结晶度 ...

1991

0.0

1992

0.0

1993

0.0

1986

0.0

1996

0.0

2011

0.0

... 晶型^[31] ...

2006

0.0

2006

0.0

2016

0.0

Cai

L. H

. , Zhang

. , Guo

B. H

. , Xu

. , Huang

Z. Y

. , Acta Polym. Sin. , 2016, (3), 382—390

(蔡利海, 张诚, 郭宝华, 徐军, 黄忠耀. 高分子学报, 2016, (3), 382—390)

The stress relaxation behavior of nylon 1010 samples with the initial strain of 1%,2.8% and 5.1% were investigated under various temperatures for not less than 10 h.The samples were measured at 20,40,60 and 80 ℃ separately.The stress relaxation rate,the residual stress and the activation volume under different experimental conditions were obtained.The results show that there was a certain permanent residual stress in the relaxation process.The reason is that the effect of the crystalline regions in the semi-crystalline nylon leads to a permanent modulus of the system.During the relaxation process,nylon samples with different initial strains showed similar trends.When the relaxation rate reached the maximum,the values of activation volume remained constant for a short period of time,which is in accordance with the principle of stress-aided thermal activation.At this stage the activation unit of the polymer was relaxed,and the relaxation rate -d σ /d t and the effective stress σ * showed an exponential relation.With further relaxation,the stress decreased to a certain threshold,activation volume would gradually increase and the independent movement of activation unit was restricted.The internal stress of the polymer gradually relaxed by the cooperative movement of multiple activation units.At this final stage,the value of stress assisted work was constant.The relaxation rate -d σ /d t and the effective stress σ * exhibited power-law relation and the power exponent is σ * V /( kT ).

1. Department of Chemical Engineering, Key Lab of Advanced Materials of Ministry of Education, Tsinghua University, Beijing 100084; 2. Institute of Petroleum, General Logistics Department, PLA, Beijing 102300

尼龙 1010 样品在初始应变为 1%、2.8%和 5.1%的条件下,在不同的恒温环境中分别进行不少于 10 h 的应力松弛实验,得到 20~80 ℃ 范围的应力松弛曲线.研究了不同应力、温度下的应力松弛速率、松弛过程的残余应力、活化体积以及相关参数的数学关系.结果表明,尼龙样品在松弛过程中存在一定的形变残余应力,体系存在恒定的长时模量.不同初始应变的尼龙样品松弛过程表现出相似的规律,当松弛速率 -d( σ / σ 0 )/dln t 达到最大值后,在一段时间内聚合物内部活化单元发生松弛, -d σ /d t 与作用于样品的有效应力 σ * 为指数关系.随着松弛过程的进行,应力减小到一定程度后,活化体积 V 逐渐增加,此时独立的活化单元运动受到限制,聚合物内部依靠多个活化单元的协同运动将内应力逐渐松弛,应力辅助功 Vσ * 为常数,-d σ /d t 与 σ * 满足幂律关系,幂指数为 σ * V /( kT ).

... 2 应力松弛曲线的时间-温度叠加方法应力松弛曲线参考文献[34]中的数据 ...

... 为了增加不同温度下曲线的重合区域, 参考文献[34]实验方法在323 K时进行了初始应变为1 ...

... 1 样品松弛前后的结构表征对于半晶型聚合物, 在采用时温等效原理进行松弛曲线的叠加时, 应尽量减小松弛前后样品取向程度和结晶度等聚集态结构的变化^[37], 因此样品在松弛实验之前进行了退火处理, 并且实验时将初始应变控制在应力-应变曲线的线性区域^[34] ...

... 此外, 在温度为 318 K 附近的尼龙1010玻璃化转变温度区^[34], 图5中曲线没有出现明显的吸热峰, 与图2中线膨胀曲线没有突然转折的现象相对应, 说明样品在松弛实验前的热处理提高了聚集态结构的稳定性 ...

... 这是由于在松弛的初始阶段, 应变刚刚达到预定值, 样品处于由强制拉伸到突然静止的状态, 分子链在失去了强制的拉伸应力时, 产生很大的反作用力, 松弛速率快速增加至最大值^[34] ...

... 原因是随着初始应变的增加, 样品受到的应力更大, 强迫聚合物内部的运动单元越过能垒发生松弛, 即松弛克服的能垒降低, 表观活化能呈现出逐渐降低的趋势, 与应力辅助的热活化理论相对应^[34] ...

... 4 松弛主曲线的应力辅助功分析研究^[34]发现尼龙1010在应力松弛过程中会先后呈现2种机理: (1) 松弛的初始阶段, 应力有助于聚合物运动单元能垒的降低, 松弛行为满足应力辅助热活化理论 ...

... 0 MPa^[34] ...

2017

0.0

1950

0.0

1960

0.0

... 研究发现, 半晶型聚合物在满足一定条件后也可以使用该方法^[37,40] ...

1959

0.0

1958

0.0

1958

0.0

... 研究发现, 半晶型聚合物在满足一定条件后也可以使用该方法^[37,40] ...

1965

0.0

... 目前, 时间-温度等效叠加方法已经广泛应用于半晶型聚合物的应力松弛研究^[41,45] ...

1967

0.0

2005

0.0

2013

0.0

2015

0.0

... 目前, 时间-温度等效叠加方法已经广泛应用于半晶型聚合物的应力松弛研究^[41,45] ...

2010

0.0

... 对于膨胀系数较小的各向同性材料, 体积膨胀系数可按线膨胀系数的3倍计算^[46], 实验中通过测试线膨胀系数来计算#cod#x003b2 ...

2003

0.0

... 曲线经高斯拟合后计算^[47]得到的取向度列于表1 ...

1992

0.0

... 这种现象与Hejlova等^[8]和Gupta等^[48]的实验结果相同 ...

1955

0.0

... 说明了在玻璃化转变温度前后应力松弛的机理并不相同, 依据阿累尼乌斯方程^[49], 相应计算出的松弛过程中与温度相关的表观活化能也会有所差别 ...

... 为松弛过程中的表观活化能, 表示松弛过程中的温度依赖性^[49] ...

1986

0.0

... 其中应力辅助功为活化体积与松弛过程中真应力的乘积, 活化体积^[50]的计算如下: ...

... V_a为应力辅助功, 指聚合物运动单元从当前位置跃迁到下一位置时应力所做的功^[50] ...