引用本文
马兰, 容婧婧, 朱有亮, 黄以能, 孙昭艳. 软胶体粒子形成束晶的动力学模拟[J]. 高等学校化学学报, 2019,40(1): 195-200.
MA Lan, RONG Jingjing, ZHU Youliang, HUANG Yineng, SUN Zhaoyan. Simulation on the Dynamic Process of Formation of Particle Cluster by Generalized Exponential Model† [J]. Chemical Journal of Chinese Universities, 2019,40(1): 195-200.
Doi:10.7503/cjcu20180323  
Permissions
Copyright©2019, 《高等学校化学学报》编辑部
版权所有
软胶体粒子形成束晶的动力学模拟
马兰1,2, 容婧婧1,2, 朱有亮2, 黄以能1,3, 孙昭艳1,2
1. 伊犁师范学院物理科学与技术学院, 新疆凝聚态相变与微结构实验室, 伊宁 835000
2. 中国科学院长春应用化学研究所, 高分子物理与化学国家重点实验室, 长春 130022
3. 南京大学物理学院, 固体微结构物理国家重点实验室, 南京 210093

联系人简介: 朱有亮, 男, 博士, 副研究员, 主要从事软物质体系的多尺度模拟研究. E-mail: youliangzhu@ciac.ac.cn

收稿日期: 2018-04-25
基金资助: 国家自然科学基金(批准号: 21774129, 21474111, 21790340, 11664042)和伊犁师范学院研究生课题(批准号: 2016YSY025)资助.
摘要

利用广义指数模型描述软胶体粒子, 结合分子动力学模拟研究软胶体粒子形成束晶的动力学过程. 通过等温压缩和等密度降温2个不同的过程, 研究了束晶形成过程中结构变化特征和动力学路径对结构的影响规律. 研究发现, 与蒙特卡洛模拟结果相比, 分子动力学模拟得到的结构随着密度的变化有明显的迟滞现象, 这是由于考虑了真实的动力学因素引起的差异. 此外, 在相同温度和压力下通过不同的动力学路径得到的相结构不完全相同, 这是由于动力学形成过程会对相结构产生很大的影响.

关键词: 软粒子束晶; 分子动力学模拟; 广义指数模型; 面心立方; 体心立方
中图分类号:O631 文献标志码:A
Simulation on the Dynamic Process of Formation of Particle Cluster by Generalized Exponential Model†
MA Lan1,2, RONG Jingjing1,2, ZHU Youliang2,*, HUANG Yineng1,3, SUN Zhaoyan1,2
1. Xinjiang Laboratory of Phase Transitions and Microstructures in Condensed Matter Physics,College of Physical Science and Technology, Yining 835000, China
2. State Key Laboratory of Polymer Physics and Chemistry, Changchun Institute of Applied Chemistry,Chinese Academy of Sciences, Changchun 130022, China
3. School of Physics, National Laboratory of Solid State Microstructures, Nanjing University, Nanjing 210093, China
Fund:† Supported by the National Natural Science Foundation of China(Nos.21774129, 21474111, 21790340, 11664042) and the Graduates’ Research Project of Yili Normal University, China(No.2016YSY025).
Abstract

The generalized exponential model was used to describe the interaction between soft colloidal particles. The dynamic process of structure formation and transformation was investigated by molecular dynamics simulations. The characteristics of the structural transformation and the influence of thermodynamicpath on the final formed structure of cluster crystal were studied for two thermodynamic paths, isothermal compression and equidensity cooling, respectively. Compared with Monte Carlo simulation results, the structure transitionin molecular dynamics simulation has obvious hysteresis on changing density, which is due to a high free energy barrier between fcc2 and fcc3 structures. In addition, the phase structure under the same temperature and pressure is not exactly same through different thermodynamic paths.It is concluded that the dynamic formation process has a great influence on phase structure.

Keyword: Soft particle cluster crystal; Molecular dynamics simulation; Generalized exponential model function; Face-centered cubic; Body-centered cubic

软胶体粒子体系具有丰富而复杂的相行为, 在外部条件改变时, 软胶体粒子可处于液态、 固态或液固共存态. 通过改变温度和密度, 软胶体粒子不仅具有从液态到固态的一阶相变, 还具有重入熔融和同态结构转变等相行为[1]. 超软的胶体粒子还可以形成束晶(Cluster crystal), 这是一种由多个胶体粒子占据同一晶格的晶体结构[2, 3, 4, 5, 6, 7]. 在束晶的1个粒子束中, 胶体粒子的质心位置并没有完全重叠, 即使胶体粒子表现出非同寻常的软化性质, 其质心重叠度仍然是有限度的[8]. 在实际生活中也存在许多类似的束晶结构, 比如由颗粒团簇形成的面心立方(fcc)或体心立方(bcc)晶体[9, 10, 11]. 由于束晶的独特性质, 其一经发现就引起了软物质领域的广泛研究兴趣[12, 13, 14, 15, 16, 17]. 许多研究者利用软势能形式(如高斯势、 简谐势和赫兹势等)来描述软粒子, 并用计算机模拟手段研究了其相行为[4, 18~21]. Miyazaki等[20]利用分子动力学模拟研究了广义赫兹势相互作用的超软粒子在低温和不同密度下形成不同粒子束结构, 以及在流体相中发生的相转变. 张凯等[7]利用蒙特卡洛模拟绘制了广义指数模型粒子的相图. 目前的研究表明, 软粒子丰富的相行为与其势能形式息息相关. 当粒子质心重合时对于一个相互作用势能达到最大值的软势, 如果傅里叶变换后只有实部, 体系随着密度的增高, 会出现重入熔融现象; 如果傅里叶变换后有虚部, 所有的温度下都没有重入熔融现象, 而在高密度下会形成束晶[4].

目前的研究多集中在束晶的结构和相行为等方面, 对于束晶形成的动力学过程, 以及调控动力学过程对结构的影响规律还不是很清楚. 本文利用广义指数模型(GEM), 研究束晶形成和结构转变的动力学过程. 广义指数模型定义为 φ(r)=εexp[-(r/σ)n], n> 2, ε 和σ 分别为能量和长度[2, 6, 7, 22]. 本文利用分子动力学模拟, 对GEM(n=4)模型粒子体系进行等温压缩和等压降温2个不同热力学路径的退火, 研究束晶形成过程中粒子束和晶体结构出现的先后顺序; 通过与蒙特卡罗模拟结果相比, 明晰动力学过程对束晶结构的影响. 以期揭示束晶的形成动力学过程, 为软粒子胶体的结构调控提供帮助.

1 模型及研究方法

分子动力学(MD)模拟是原子、 分子水平上的计算机模拟方法, 该方法基于牛顿力学, 通过求解运动方程来精确得到原子或分子在不同时刻的位置和速度, 进而获得计算体系热力学量和其它宏观量[23, 24]. 假设1个含有N个粒子的体系, 粒子之间相互作用势是位置的函数U(r1, r2, …, rN), 根据经典力学可知体系中任一粒子所受的力为势能的梯度:

F→i=-∇iU=-i→∂/∂xi+j→∂/∂yi+k→∂/∂ziU(1)

由牛顿运动定律可得i粒子的加速度为

a→i=F→i/mi(2)

求解运动方程获得粒子不同时刻的速度和位置. 分子动力学模拟过程如下: 首先由体系粒子的位置计算体系的作用势, 再由式(1)和式(2)计算各粒子的加速度, 然后选取1个小的δ t并采取合适的算法解运动方程, 获得经过δ t后各粒子的位置和速度. 重复以上步骤获得经过2δ t后粒子的位置和速度, 如此反复, 可得到各时间下体系中粒子的运动轨迹及速度信息, 由此获得相关表征量.

采用分子动力学模拟方法, 在NVT系综下, 用速度Verlet法积分牛顿运动方程. 温度由Nosé -Hoover 热浴控制[24], 模拟中采用的时间步长为0.001. 为了获得可靠的结果, 每106时间步记录一次体系的物理性质. 分子动力学模拟使用大尺度的GPU加速的GALAMOST 软件包[25]. 该体系包含4096个胶体粒子, 使用GEM(n=4)模型描述胶体粒子之间的相互作用. 约化温度定义为T=kBT/ε , ε 为能量的基本单位. 模型中σ =1.0, ε =1.0, 粒子之间相互作用的截断半径rc=2.0. 在高斯势下, 通过改变体系的密度和温度考察胶体粒子形成束晶的动力学过程. 等温压缩和等密度降温的热力学路径由基于蒙特卡罗模拟绘制的GEM-4的相图(图1)中给出.

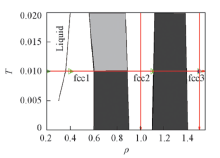Fig.1 Thermodynamic processpaths of isothermal compression and equidensity cooling on GEM4 phase diagram

为了对模拟结果进行有效分析, 计算了体系的有序度和排列结构. 传统意义上的共近邻方法(CAN)对于分析fcc、 bcc和密排六方(HCP)等结构是非常有效的手段. 该方法通过设定截断半径能清楚地提供局部粒子排列的信息, 从不同晶型粒子体系中分辨出结晶缺陷. 但是, 在多相体系中, 由于全局定义的截断半径的选择性不是特别明确, 使得这类传统CAN方法并不适用于多相体系. 因此, 在本文模拟体系中, 采用OVITO软件自带的自适应方法(a-CAN)分析体系粒子排列情况. 自适应a-CNA方法是传统CNA方法的衍生物, 主要用于分析多相体系. 通过事先指定体系中每一个粒子的截断半径, 并通过与参照结构比较来自动调整每个粒子的截断半径, 进而分析体系局部粒子的排列信息[26]. 利用键取向序参量(BOO)表征粒子与其近邻之间相对位置的取向特性, BOO也被称为Steinhardt有序参数, 通常用于确定分子模拟中的晶体结构. 尤其是Q4和Q6常被用作区分立方和六方结构的最优选择[27].

2 结果与讨论
2.1 等温压缩过程模拟

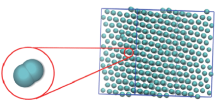
将模拟盒子的大小设定为27× 27× 27, 盒子中包含的粒子数N=4096. 在体系温度恒定为0.01时, 对盒子进行压缩, 即增大体系的密度, 观察胶体粒子在超软势作用下形成结构及结构演化的动力学过程. 图2是最终形成的结构. 随着密度的增大, 胶体粒子的结构由最初的无序液态逐渐变得有序并且进一步形成规则的晶体. 经结构分析发现, 这是由单粒子组成的面心立方(fcc1)晶体结构.

Fig.2 Simulation snapshot of fcc2 of GEM-4 system at ρ =1

继续增加密度, 单粒子晶体逐渐转变成二聚体的晶体. 当密度增加到1.0左右时, 体系完全演化成二聚体的面心立方(fcc2)晶体结构. 该结果与文献[7, 18]的研究结果非常吻合. 如图3所示, 此动力学过程中束晶的类型随着密度增大而改变. 尤其是当ρ > 0.9时, 软粒子束晶的聚集状态发生了突变, 单粒子数减少, 二聚体数目增加. ρ =0.94是二聚体和单粒子数量之间转换的临界值, 当ρ > 0.94时二聚体的数目超过单粒子的个数, 体系以二聚体为主体. 随着ρ 增加, Q4和Q6值发生变化(Q4和Q6判断晶体结构的依据参考文献[27]). 在ρ =0.57~0.70范围内, 体系属于fcc晶体. 从ρ =0.70增加到ρ =0.95, 体系经历了两相共存区. 在这一过程中fcc晶体经历了1个不连续的同构相变[28, 29, 30]. 在ρ =0.7~1.0之间, 聚集状态由单粒子转换成二聚体, 且fcc晶体的同构转变为部分bcc晶体类型. 当ρ =1时, 体系主体为二聚体的fcc2晶型. 与蒙特卡洛模拟得到的结果相比, 分子动力学过程中发生的一系列结构的转变具有明显的迟滞现象. 这是由于动力学因素对体系的影响[31]. 由于在共存相及其附近成核的自由能垒较高, 因此在较短的动力学模拟时间内很难观察到相转变现象, 因此导致了迟滞效应[24].

Fig.3 Cluster size(A) and Q4(a) and Q6(b)(B) vs. densities
Inset of (A): a-CAN analysis by OVITO.

当温度恒定为0.01时, 对体系进行等温压缩, 使ρ 从0.1变化到1.5, 体系结构随着密度的变化过程如图4所示. 红色粒子是被标记的粒子, 利用示踪粒子的方法, 给出不同密度下束晶形成过程中粒子聚集状态以及体系的结构演化过程(图5), 在此动力学过程中, 体系密度在ρ =1.1~1.45之间, 单粒子、 二聚体以及三聚体的数量均发生了转变. 密度在ρ =0.7~0.85之间结构属于fcc晶体. 在ρ =0.85~1.4之间, Q4和Q6出现了2次降低, 分别对应聚集体类型的变化. 此时的晶体结构主要为fcc和bcc两相共存区, 且fcc晶体逐渐向bcc晶体的结构转变. 从图5可以看出, 体系的晶体最终不能完全转化成三聚体的面心立方(fcc3)结构, 而是形成了二聚体的体心立方(bcc2)晶体结构. 这一结果与随机蒙特卡罗模拟方法得到的结果明显不同. 这可能是由于fcc2与fcc3结构之间的自由能垒较高, 因而采用动力学方法难以获得热力学平衡态结构. 此外, 还观察到三聚体的形成有3种过程: (1) 由3个单粒子聚集形成; (2) 由1个二聚体和另一个二聚体融化后分离出的单粒子组成; (3) 由1个单粒子和1个二聚体聚集形成. 经数据分析发现, 第3种的形成方式占主导.

Fig.4 Snapshots at different densities
(A) ρ =0.2; (B) ρ =0.4; (C) ρ =1.1; (D) ρ =1.5.

Fig.5 Cluster size(A) and Q4(a) and Q6(b)(B) vs. densities
Inset of (A): a-CAN analysis by OVITO.

2.2 等密度降温过程模拟

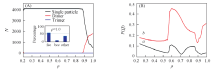
为了全面理解胶体粒子在高斯软势中的重入熔融以及同构转变的现象, 控制模拟体系的密度为ρ =1, 对体系进行降温处理(T=1.0→ 0.01), 观察模拟体系形成的晶型结构, 结果如图6所示. 随着温度的降低, 单粒子数目迅速降低, 二聚体数目迅速增加, 且在T≈ 0.8时二聚体数目大于单粒子数目, 表明此时体系中粒子的主要存在状态为二聚体. 当T=0.65时, Q4和Q6值迅速增加, 且体系由无序的聚集体转变成有序的fcc晶型. 当温度进一步降低到T≈ 0.08时, Q4和Q6略微降低, 表明体系中的晶体有序度下降. 结合OVITO的a-CAN分析可知, 此时体系主要以fcc晶型填充. 根据图6给出的在相同密度条件下Q4和Q6以及聚集体形态随温度降低的变化过程可知, fcc2晶体的形成过程为先发生从单粒子到二聚体的转变, 进而二聚体逐渐聚集形成有序的fcc2晶体.

Fig.6 Cluster size(A) and Q4(a) and Q6(b)(B) vs. temperatures
Inset of (A): a-CAN analysis by OVITO.

当ρ =1.5时, 对体系进行缓慢降温, 温度从1.0降低到0.01, 观察体系的变化, 结果如图7所示.

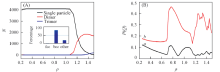
Fig.7 Snapshots at different temperatures
(A) T=0.9; (B) T=0.09; (C) T=0.06; (D) T=0.01.

红色粒子是被标记的粒子, 利用示踪粒子的方法, 粒子束在不同温度下的聚集状态以及体系的结构变化过程如图8所示. 体系经历了无序的聚集体到有序的晶体的变化过程. 由聚集体形态以及Q4, Q6随着温度降低的变化过程发现, 在温度为0.8时体系中的二聚体和三聚体类型的数量发生转变, 且三聚体的数目迅速超过了二聚体和单粒子的数目. 在相同温度下, Q4和Q6也迅速增大, 体系的聚集态结构为fcc晶型. 结合OIVTO的a-CAN分析, 可以判断出体系中的三聚体所属类型为fcc晶体以及少部分其它晶型的混合物. 温度进一步降低至0.65时, 体系基本由fcc3晶体构成. 比较等密度降温和等温压缩得到的结果发现, 在相同温度和压力下通过不同的热力学路径得到的相结构不完全相同, 这可能是由于不同有序结构之间的自由能垒较高, 采用动力学方法难以逾越较高的自由能垒, 因而无法达到最终的热力学平衡态结构. 因此, 需要采用增强抽样等方法才能获得热力学平衡态的结构.

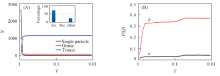Fig.8 Cluster size(A) and Q4(a) and Q6(b)(B) vs. temperatures
Inset of (A): is a-CAN analysis by OVITO.

综上所述, 采用分子动力学模拟方法研究了软胶体粒子体系形成束晶的动力学过程, 探讨了等温压缩和等密度降温2个不同的热力学路径下, 胶体粒子形成有序束晶的动力学差异. 随着密度的改变, 体系结构经历“ 无序→ fcc1→ fcc2和bcc共混物→ fcc2→ bcc2” 的变化过程, 粒子形态从单粒子向二聚体转变. 与蒙特卡洛模拟结果相比, 分子动力学模拟得到的结构随着密度的变化有明显的迟滞现象. 模拟等密度降温过程发现, 该体系的结构变化为“ 无序的聚集体→ fcc2→ fcc3” . 从等温压缩和等密度降温2个不同的热力学路径得到的结果不完全相同. 在相同密度和温度下, 通过等温压缩得到的结构是bcc2, 而通过等密度降温或者蒙特卡罗模拟得到的结构是fcc3. 因此, 动力学过程会对模拟结果产生很大的影响, 甚至得到不同的结构. 这是由于形成fcc3所需的自由能垒较高, 而分子动力学模拟使得体系无法克服较高的自由能垒, 因而无法获得热力学更加稳定的fcc3结构.

参考文献
[1] Young D. A. , Alder B. J. , J. Chem. Phys. , 1979, 70(1), 473—481 [本文引用:1]
[2] Coslovich D. , Strauss L. , Kahl G. , Soft　Matter, 2011, 7(5), 2127—2137 [本文引用:2]
[3] Lascaris E. , Malescio G. , Buldyrev S. V. , Stanley H. E. , Phys. Rev. 　E, 2010, 81(3), 031201 [本文引用:1]
[4] Likos C. N. , Lang A. , Watzlawek M. , Löwen H. , Phys. Rev. 　E, 2001, 63(3), 031206 [本文引用:3]
[5] Miller W. L. , Cacciuto A. , Soft　Matter, 2011, 7(16), 7552—7559 [本文引用:1]
[6] Moreno A. J. , Likos C. N. , Phys. Rev. 　Lett. ,2007, 99(10), 107801 [本文引用:2]
[7] Zhang K. , Charbonneau P. , Mladek B. M. , Phys. Rev. 　Lett. ,2010, 105(24), 245701 [本文引用:4]
[8] Klein W. , Gould H. , Ramos R. A. , Clejan I. , Mel'cuk A. I. , Physica　A, 1994, 205(4), 738—746 [本文引用:1]
[9] Bernabei M. , Bacova P. , Moreno A. J. , Narros A. , Likos C. N. , Soft　Matter, 2013, 9(4), 1287—1300 [本文引用:1]
[10] Lenz D. A. , Blaak R. , Likos C. N. , Mladek B. M. , Phys. Rev. 　Lett. ,2012, 109(22), 228301 [本文引用:1]
[11] Sciortino F. , Zaccarelli E. , Nature2013, 493(7430), 30—31 [本文引用:1]
[12] Ikeda A. , Miyazaki K. , Phys. Rev. Lett. ,2011, 106(1), 015701 [本文引用:1]
[13] Lang A. , Likos C. N. , Watzlawek M. , Löwen H. , J. Phys. : Condens. 　Matter, 2000, 12(24), 5087—5108 [本文引用:1]
[14] Likos C. N. , Soft　Matter, 2006, 2(6), 478—498 [本文引用:1]
[15] Malescio G. , J. Phys. : Condens. Matter, 2007, 19(7), 073101 [本文引用:1]
[16] Prestipino S. , Saija F. , Giaquinta P. V. , Phys. Rev. E, 2005, 71(5), 050102 [本文引用:1]
[17] Slimani M. Z. , Bacova P. , Bernabei M. , Narros A. , Likos C. N. , Moreno A. J. , ACS Macro. Lett. ,2014, 3(7), 611—616 [本文引用:1]
[18] Bianca M. M. , Patrick C. , Christos N. L. , Daan F. , Gerhard K. , J. Phys. : Condens. Matter, 2008, 20(49), 494245 [本文引用:2]
[19] Likos C. N. , Mladek B. M. , Gottwald D. , Kahl G. , J. Chem. Phys. , 2007, 126(22), 224502 [本文引用:1]
[20] Miyazaki R. , Kawasaki T. , Miyazaki K. , Phys. Rev. 　Lett. ,2016, 117(16), 165701 [本文引用:1]
[21] Mladek B. M. , Charbonneau P. , Frenkel D. , Phys. Rev. Lett. ,2007, 99(23), 235702 [本文引用:1]
[22] Mladek B. M. , Gottwald D. , Kahl G. , Neumann M. , Likos C. N. , Phys. Rev. 　Lett. ,2006, 96(4), 045701 [本文引用:1]
[23] Allen M. P. , Tildesley D. J. , J. Computer Simulation of Liquids, Oxford University Press, Oxford, 1987 [本文引用:1]
[24] Frenkel D. , Smit B. , Understand ing Molecular Simulation: from Algorithms to Applications, Academic Press, San Diego, 2002 [本文引用:3]
[25] Zhu Y. L. , Liu H. , Li Z. W. , Qian H. J. , Milano G. , Lu Z. Y. , J. Comput. Chem. ,2013, 34(25), 2197—2211 [本文引用:1]
[26] Alexand er S. , Modell. Simul. Mater. Sci. Eng. , 2012, 20(4), 045021 [本文引用:1]
[27] Lechner W. , Dellago C. , J. Chem. Phys. ,2008, 129(11), 114707 [本文引用:2]
[28] Pàmies J. C. , Cacciuto A. , Frenkel D. , J. Chem. Phys. ,2009, 131(15), 159903 [本文引用:1]
[29] Stillinger F. H. , J. Chem. Phys. , 1976, 65(10), 3968—3974 [本文引用:1]
[30] Tim N. , Christos N. L. , J. Phys. : Condens. Matter, 2011, 23(23), 234112 [本文引用:1]
[31] Marta M. S. , Arash N. , Gerhard K. , J. Phys. : Condens. Matter, 2013, 25(19), 195101 [本文引用:1]