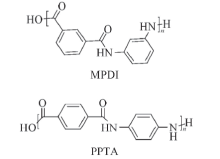
基团贡献法^[13]主要使用Materials Studio(MS)软件中的Synthia模块. 首先建立MPDI和PPTA的重复结构单元(其结构式如图1所示), 在Forcite模块中进行几何优化, 再用Synthia模块进行计算, 温度设置为300 K, MPDI和PPTA的分子量都设置为952~95200, 即聚合度为4~400, 从计算的数据中获得高分子的T_g与分子质量.

Fig.1

	Figure Option ViewDownloadNew Window
	Fig.1 Chemical structures of MPDI and PPTA

分子动力学模拟方法主要参考了Pant等^{[14, 15, 16]}的工作, 主要涵盖以下步骤(具体的参数设定则根据体系的不同各异): (1) 建立聚合物重复单元并优化结构; (2) 构建聚合物的单链结构并优化模型; (3) 建立无定形结构(Amorphous cell); (4) 退火(Anneal); (5) 分子动力学(NVT, NPT); (6) 性能参数(Analysis).

使用Materials Studio软件中的Dynamics模块进行模拟. 首先, 建立MPDI和PPTA的结构单元, 考虑到聚合物的分子量对其玻璃化温度有很大的影响, 在MD模拟过程中, 建模时应充分考虑聚合度的合理设定使模型具有代表性, 参考了GC法的分子量与T_g的关系曲线, 分别构造聚合度为100的MPDI和聚合度为100的PPTA的单链模型, 并对所建模型进行结构优化, 步数为20000步, 力场选用COMPASS力场^{[17, 18, 19, 20, 21, 22, 23]}, 范德华力使用Atom-based方法, 静电作用使用Group-based方法, 其中Quality选择Ultra-fine, 非键截断半径取1.85 nm, 样条宽度为0.1 nm, 缓冲宽度为0.05 nm. Algorithm选择Smart对聚合物单链的电荷和能量进行平衡优化.

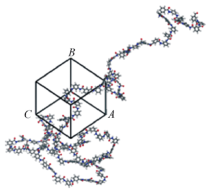
Smart运算作为一种有效使系统达到平衡的运算方法, 综合了Steepest descent, ABNR和Quasi-Nowton 3种运算. 优化完成后, 使用Amorphous cell模块建立密度为0.6 g/cm³的MPDI单链无定形单胞模型和密度为0.4 g/cm³的PPTA单链无定形单胞模型(图2), 并对所建的模型进行20000步的结构优化(模拟参数同上). 初始建模密度选择0.6 g/cm³的MPDI和0.4 g/cm³的PPTA的原因是为了避免在建模过程中密度设置过高导致分子链太过拥挤而相互缠结, 进而导致体系能量过高而无法建立单胞模型.

Fig.2

	Figure Option ViewDownloadNew Window
	Fig.2 Amorphous cell construction for a MPDI

使用Forcite模块中的Anneal进行退火动力学模拟, 为了得到真实可靠的聚合物结构, 选择在0.0001 GPa, 300 K下运行1000 ps的NPT退火分子动力学模拟, 共进行20个循环温度, 温度梯度为25 K, 每个循环从300 K升温到1000 K再降温到300 K的退火处理, 退火的目的是为了消除由于在建模过程中产生的局部不合理的结构, 为下一步动力学模拟提供合理的构象.

分子动力学模拟选择Nose-Hoover控温, 这种控温并不能改变系统平衡, 但可以有效维持系统的平衡, 这个设置描述原子运动更为真实, 并且可以调整聚合物分子链的构象. 压力的控制采用Berendsen控压. 第1步进行NVT系综动力学模拟, 时间为100 ps, 使高分子链进一步松弛; 第2步进行时间为200 ps的NPT系综的动力学模拟, 系统达到平衡, 得到系统平衡时的密度并分析、 采集数据. 分子动力学模拟初始阶段温度设为700 K, 每个阶段实验完成以后温度将依次降低20 K, 并且上一阶段(较高温度)的动力学最终平衡构象作为下一阶段(较低温度)分子动力学模拟的初始构象, 直到实验温度下降到440 K为止, 实验温度范围为700~440 K, 共进行14组实验, 从建模到动力学模拟结束的总模拟时间为6.6 ns, 体系达到平衡.

使用基团贡献法测得聚合度为100时MPDI和PPTA的T_g趋于平衡, 此时对应的T_g分别为524.5 K和583.8 K. 使用分子动力学模拟, 当系统到达平衡后分别用密度-温度法、 比体积-温度法、 回转半径-温度法和能量-温度法分析可得到聚合物的玻璃化转变温度. 模拟结果与实验值列于表1.

Table 1

Table 1

Table 1 Tg of MPDI and PPTA from different methods Method Tg(MPDI)/K Tg(PPTA)/K Experiment value 545.2— 548.2 600— 618.2 GC 524.5 583.8 MD(Density-Temperature) 565.2 616.5 MD(Specific volume-Temperature) 566.9 616.3 MD(Radius of gyration-Temperature) 571.3 615.8 MD(Non-bond energy-Temperature) 567.4 617.4

Table 1 Tg of MPDI and PPTA from different methods

表1结果表明, 基团贡献法模拟所得的T_g较实验值低, 而分子动力学模拟所得的T_g较实验值高. MPDI和PPTA实验所测的真实T_g介于基团贡献法和分子动力学法模拟值之间.

通过对比2种模拟方法及实验所得T_g的数值, 发现基团贡献法和MD模拟计算得到的聚合物的T_g与实验数据接近, 这说明2种模拟方法均可以用来模拟真实状态下MPDI和PPTA的T_g, 表明使用基团贡献法和分子动力学预测全芳香性的聚酰胺T_g具有合理性.

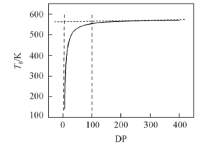
基团贡献法是使用定量结构-性能关系来预测聚合物性质的方法, 通过Synthia模块计算不同聚合度(DP)的PPIA的T_g, 计算结果使用Origin软件作图, 得到PPIA的T_g与聚合度的关系如图3所示.

Fig.3

	Figure Option ViewDownloadNew Window
	Fig.3 Tgvs. degree of polymerization(DP) chart for PPIA at 300 K

从图3可以看出, 聚合物的T_g随着聚合度的增加而增加, 当聚合度达到某个值时, T_g达到了一个平台区, 不再发生显著变化. 由图3可见, 当聚合度达到100时, PPIA的T_g已经非常接近平台区的数值, 此时对应的T_g为554.4 K.

考虑到在进行分子动力学模拟时, 计算时间与体系中的原子数目有关. 原子数目增加, 模拟时间将大大增加, 并且原子数目越多, 模拟体系就越复杂, 建立无定形结构模型越困难, 因此在后续的分子动力学模拟中, 选取聚合度为100的PPIA作为分子动力学模拟的模型.

2.2.1 平衡的判定 分子动力学模拟体系的平衡需要足够的模拟时间, 只有模拟体系达到平衡才能获得可靠有效的模拟数据. 判定分子动力学模拟达到平衡的条件^{[25, 26]}主要有以下两方面: 首先温度需处于平衡状态, 要求温度在平衡值上下波动, 其波动的标准偏差应该小于10 K; 其次能量也需处于平衡状态, 要求能量沿平衡值上下波动或者恒定. 图4为PPIA在500 K和200 ps的NPT系综状态下温度与能量的平衡图, 可见, PPIA的分子动力学模拟体系已经达到平衡.

Fig.4

	Figure Option ViewDownloadNew Window
	Fig.4 Temperature(A) and energy fluctuation properties(B) vs. simulation time of PPIA(500 K, 200 ps NPT)

2.2.2 PPIA的密度与温度之间的关系 通过分子动力学模拟得到PPIA的密度-温度关系(图5). 由图5可以看出, T_g将260 K的温差范围分成2个温度区间, 这2个温度区间内的密度与温度呈线性变化, 根据2个温度区间的数据进行线性拟合, 可得到2条斜率不同直线, 2条直线的交点对应的温度即为PPIA的T_g, 为593.6 K. 这种玻璃化转变可以用“ 等自由体积理论” ^{[27, 28]}来说明. 高分子的体积可以分成2个部分: 一部分为占有体积, 即为分子与原子自身体积; 另一部分被称为自由体积, 也就是分子间的空隙体积. 自由体积是以大小不一的“ 空穴” 分散在高分子中, 因此这为链段运动提供了足够的转动空间, 从而分子链可以通过转动和位移来调整构象. 自由体积理论认为, 处于T_g时, 自由体积为链段运动提供空间, 是正好处于链段可以运动或者运动被冻结这2种状态之间的临界值.

Fig.5

	Figure Option ViewDownloadNew Window
	Fig.5 Density vs. temperature chart for an MD simulation of PPIA

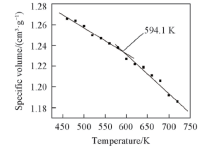
2.2.3 PPIA的比体积与温度之间的关系 通过MD模拟得到PPIA的比体积-温度关系(图6). 2个温度区间内的比体积与温度呈线性变化, 经线性拟合得到2条直线的交点, 对应的温度即是PPIA的玻璃化转变温度(594.1 K). 这种玻璃化转变同样可以用“ 等自由体积理论” 来解释.

Fig.6

	Figure Option ViewDownloadNew Window
	Fig.6 Specific volume vs. temperature chart for an MD simulation of PPIA

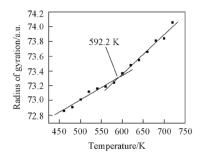
2.2.4 PPIA的回转半径与温度之间的关系 聚合物是通过小分子聚合而成的, 因此聚合物单键仍能内旋转, 而正因为这种内旋转导致聚合物拥有许多不同的构象. 众所周知, 分子不停地进行热运动, 而这种热运动可以使分子的构象发生改变, 由于构象发生了改变, 聚合物分子尺寸也会发生相应的改变. 在高分子中, 通常使用均方回转半径来表征分子尺寸. 由于均方回转半径的大小可以用来表征聚合物分子链柔顺性的大小, 而聚合物的玻璃化转变又和链的柔顺性有直接关系^[25]. 因此, 通过分子动力学模拟, 对不同温度下PPIA的回转半径和温度进行了分析(图7).

Fig.7

	Figure Option ViewDownloadNew Window
	Fig.7 Radius of gyration vs. temperature chart for an MD simulation of PPIA

由图7可见, PPIA的回转半径随温度的升高而升高. 随着温度升高, 聚合物的自由体积和分子所占据的体积都会发生膨胀, 因此分子间距离将会逐渐增大, 从而导致回转半径也会增大. 通过线性拟合PPIA的回转半径与温度图, 可以得到PPIA的T_g为592.2 K. 分析结果说明, 通过回转半径与温度变化关系可以预测PPIA的T_g.

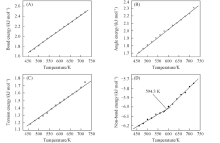
2.2.5 PPIA的力场能量与温度之间的关系 在分子力学原理中, 通常力场的总能量可以简单地分成3项^[26], 公式为E_total=E_valence+E_non-bond+E_crossterm, 其中, E_total为力场的总能量; E_valence为成键相互作用能; E_non-bond为非成键相互作用能; E_crossterm为交叉形式的能量. 对于成键相互作用能又可以分为键伸缩能、 键角弯曲能和扭转能等; 非成键相互作用能也可以分为范德华作用能和库仑作用能. 对PPIA的键能、 键角能、 扭转能与非键作用能与温度作图, 研究力场各能量与T_g的关系, 结果示于图8.

Fig.8

	Figure Option ViewDownloadNew Window
	Fig.8 Plots of energy components vs. temperature chart for an MD simulation of PPIA

由图8可看出, PPIA的键能、 键角能和扭转能都随温度的升高线性上升, 能量与温度的关系图中没有拐点, 由此可知键能、 键角能和扭转能在玻璃化转变时不会发生突变, 不是玻璃化转变的主要因素. 而PPIA的非键能与温度关系图中出现一个拐点, 不管在拐点之上还是在拐点之下, 随着温度降低, 非键能都直线下降, 但是处于拐点之下的直线斜率较小, 这个拐点即是PPIA的T_g, 为594.3 K. 非键能在玻璃化转变出现一个拐点的现象可以认为, 非键能可能处于T_g以下时受到限制, 对于PPIA来说, 这也是出现玻璃化转变的根本原因.

PPIA的T_g的模拟结果列于表2. 可以看到, 在分子动力学模拟中, 密度-温度法、 比体积-温度法、 回转半径-温度法和非键能量-温度法测得的PPIA的T_g的差值都不大, 基团贡献法得到的PPIA的T_g比分子动力学的5种方法所得值要低40 K左右. 基团贡献法是利用定量结构性能关系来预测聚合物的T_g, 可能是没有考虑这2种聚合物结晶的缘故; MD建立的聚合物链长模型是单分散性, 而真实情况下聚合物链长是多分散性, 由于链长的多分散性导致低分子链作为高分子量的增塑剂, 从而降低高分子的T_g; 其次, 加热/冷却的速率和时间尺度也是影响T_g的重要因素, 通常DSC测试样品的冷却速度是10 K/min, 而模拟时, 两步的温差范围是20 K, 两步的时间却为1.3 ns, 温度快速变化导致材料的变硬, 从而使T_g升高.

Table 2

Table 2

Table 2 Tg of PPIA from different methods Method Tg/K GC 554.4 MD(Density-Temperature) 593.6 MD(Specific volume-Temperature) 594.1 MD(Radius of gyration-Temperature) 592.2 MD(Non-bond energy-Temperature) 594.3

Table 2 Tg of PPIA from different methods

不管是基团贡献法, 还是分子动力学模拟, 所测得的T_g均大于500 K, 对比表1和表2可见, PPIA的T_g值介于MPDI和PPTA的T_g值之间, 能量项中引起PPIA玻璃化转变的原因同样是非键能随温度的变化. 可以合理地推断PPIA的热性能可能介于MPDI和PPTA之间, 若能纺制成纤维, 极可能发展成介于MPDI和PPTA之间的高性能聚酰胺.